Teaching the Counting On Addition Strategy? Don’t Forget to Do This.

  Counting On is a beginning mental math addition strategy. It is generally taught as an introductory mental math strategy and is usually simple for students to grasp. Many of your students are probably already using this strategy without knowing it. Counting on means that you start with the biggest number and then count up from there. For example, to add 5+3, start with the “5” and then count up, “6, 7, 8.” This is to discourage students from counting like this: “1, 2, 3, 4, 5…..6, 7, 8.” If you are working with very young students, they may need to count both sets at first, but work towards starting from the bigger number. It is also important to reinforce the commutative property of addition when working with this strategy. For example, even if students are adding “2+6,” they still should start with the bigger number. In this case we would start with “6” and count up “7, 8.” The counting on strategy should only be used for adding 1, 2, 3, or 4 to a larger number. If students try to count on with numbers higher than 4, it gets too confusing, and mistakes happen. For example, if a student tried to count on to add 15+12, he would say, “15,” and then count on: “16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27.” This is an ineffective way to add. Students will realize this once other, more efficient strategies, are discovered. Once students learn more advanced addition strategies, counting on will slowly be phased out of your students’ “addition toolbox.” But it IS an effective beginning addition strategy for young students. Here’s a video that will explain the counting on strategy in more detail: WAYS TO REINFORCE COUNTING ON Teaching math in a way that reinforces concrete, representational, and abstract thinking will pay off as your students discover new, efficient strategies. If we want our students to think flexibly and strategically, we MUST provide them with the opportunity to SEE math. Please give your students ample time to work with manipulatives such as base 10 blocks, rekenreks, and ten frames (preferably all three). Experience with these manipulatives will give your students a visual – and as they work with counting on activities, they will be able to visualize the math in their heads. Too often we skip right to the paper and pencil work when it comes to math strategies. Time to work with concrete materials is essential to your students math fluency. When you are ready for paper and pencil tasks, here are some ideas for how you can reinforce the counting on strategy in your classroom. I have also included a free download to practice this concept at the end of this post. DICE OR DOT PATTERNS When first beginning to teach counting on, dot patterns can be an effective tool. Encourage your students to say the big number and then count on from there using the dots. For example, for the first example shown below, your students should say, “19,” and then count on: “20, 21.”   TEN FRAMES To use a 10 frame, students can represent the equation with two different symbols or colors.   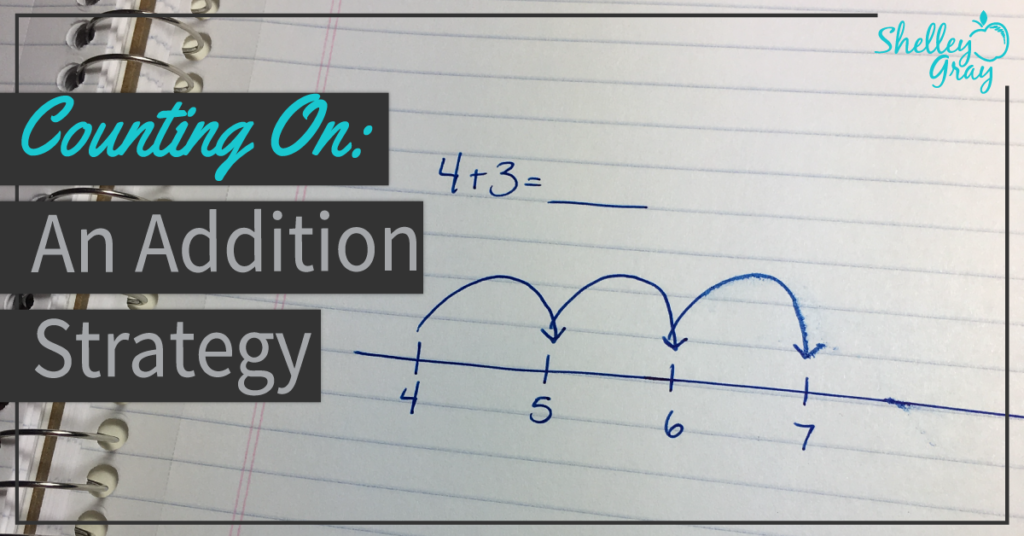NUMBER LINES Number lines are a fantastic tool for so many math concepts, so getting students started using them for beginning addition is a great idea. Encourage students to write the highest number and then use “jumps” to count on the smaller number. For the equation shown below (27+2), students would first write the 27 and then make two jumps to make a sum of 29.       NEXT STEPS:

• Find a Counting On Addition Strategy Unit here:

• If you would like full support for teaching addition strategies in your classroom, check out The Addition Station HERE.
• Download a FREE activity sheet for practicing the counting on strategy HERE.

• Find task cards to reinforce the counting on strategy in isolation here:
  • counting on task cards for 1st grade
  • counting on task cards for 2nd grade