
If you find your head spinning when you think about all the addition strategies that you should be teaching, you are certainly not alone. Although teaching addition is one of the most important math concepts that we encounter, it comes with challenges.
First of all – time. How do we find the time to do a really good job of teaching the different addition strategies so that our students possess excellent understanding, while also doing a really good job of teaching everything else in our overwhelming curriculum?
Second, differentiation. All of our students learn at different speeds and in different ways. We can’t expect them all to learn the addition facts and strategies at the same time, but how do we ensure that each student is working to his full potential?
One last big challenge is the balance between mental math strategies and memorization. We know that strategies are important. We want our students to UNDERSTAND number, rather that simply memorizing the facts. However, automaticity is important too! How can we reach this balance?
Fortunately, there are specific strategies that we can teach to make addition easier for our students, and accessible for all of them.
Before I begin – if you are looking for a resource where all of the work is done for you, you may be interested in The Addition Station, a self-paced, student-centered math station where students work through the basic addition facts and strategies, mastering each one as they go. Strategies are integrated in a strategic manner, ensuring that students build on their understanding progressively. See The Addition Station for Grades 1-2 HERE and The Addition Station for Grades 3-4 HERE.
Alright, so let’s talk about addition strategies.
Strategies are ESSENTIAL, for all operations. We want our students to be able to think flexibly about numbers, and use strategies naturally. This means that understanding is key. Automaticity (quick recall) will naturally follow.
Here are some effective strategies for addition:
Plus 1, 2, 3 and Extensions
In younger grades, we begin with the Plus 1, 2, and 3 facts. We can teach Plus 1 as 1 more, Plus 2 as 2 more, and Plus 3 as 3 more. As our students are ready for more of a challenge, we can extend these facts into the tens, hundreds, and even thousands. For example, the fact 7+1 can be extended to 70+10, 700+100, or 7000+1000. Teach your students to look for familiar facts in these bigger problems, so that when they need to solve a fact like 50+20, they think, “I know that 5+2=7, so 50+20=70.” During the extensions, be sure to emphasize place value. For example, we can think of 500+200 as 5 groups of 100 plus 2 groups of 100 to make 7 groups of 100.
Counting On
If students have been working with Plus 1, 2, and 3, they have technically already been working with the counting on strategy. Counting On is an introductory addition strategy that should only be used to add 1, 2, 3, or 4 to a number. Beyond this it gets confusing and can cause errors. To count on, we begin with the higher number and count on. For example, for 17+3, we think, “17…18, 19, 20.” For 2+34, we start with 34 and count on: “34…35, 36.” Dot patterns, ten frames, and number lines are all excellent tools for counting on. Read more about counting on, and download some free printables to help you HERE.
Extending the Doubles and Near Doubles
The doubles are typically facts that become automatic early on. The near doubles are facts like 4+5, where we encourage students to think, “I know that 4+4 is 8, and 1 more is 9.” We can also extend these facts. For example, when a student is faced with 30+30, he can think, “I know that 3+3 is 6, so 30+30 is 60.” Again in this level, we encourage students to think in groups of 10, 100, or 1000. For example, 200+200 can be thought of as 2 groups of 100 plus 2 groups of 100. Read more about extending the doubles and near doubles, and download some free printables to help you HERE.
Plus 7, 8, and 9
When we add 7, 8, or 9 to a number there are a couple of different approaches that we can use. First of all, we can add 10 and then take some away. Alternatively, we can make a 10 and then add the rest. I’ve discussed both of these approaches in detail in THIS BLOG POST. You’ll also find some free printables to help you!
Left-to-Right Addition
Left-to-right addition (also known as front-end addition or the partial sums method) is one of the most powerful mental math strategies for teaching addition of 2 or 3-digit numbers. However, many people are confused by why it is important and why it can be more effective than traditional vertical addition.
With left-to-right addition we add from left to right. So in a two-digit equation we add the tens first and then the ones. For example for 25+34 we first add 20+30 to make 50, then 5+4 to make 9, and then 50+9 to make the final sum of 59.
For a detailed explanation and rationalization of this strategy, as well as free printables to help you teach it, please see THIS POST.
Using Friendly Numbers
A friendly number is a number that is easy to work with. For example, multiples of 10 are “friendly” because they are easy to work with when we add or subtract.
When we use the “friendly number” strategy for addition, it helps us work with big numbers. This is because we are essentially breaking the equation up into more manageable parts.
We begin by getting to a friendly number, which is typically a multiple of 10, 100, or 100 – depending on the numbers that we are working with. Then we add on the remainder.
For example, for the equation 27+9, we could first get to the friendly number 30 by adding 3, and then add the remaining 6 to make 36.
For a complete, detailed explanation of the friendly number strategy for addition, as well as some free printables to help you, please see THIS POST.
Breaking Up An Addend
Breaking up, or decomposing, an addend is a fantastic mental math strategy for addition that can be used in many different circumstances. This strategy involves breaking up one of the numbers in an equation into more manageable parts. Like many other mental math strategies, this encourages students to think flexibly and to manipulate numbers in different ways. This is the big goal of mental math!
For a detailed explanation of this strategy as well as free printables to help you teach it, please see THIS POST.
Compensation
Compensation is a mental math strategy for multi-digit addition that involves adjusting one of the addends to make the equation easier to solve. Some students may prefer this strategy as an alternative to left-to-right addition or the breaking up the second number strategy.
Compensation is a useful strategy for making equations easier to solve. More importantly, it encourages students to think flexibly about numbers.
Let’s solve the equation 34+49 using the compensation strategy.
First, since 49 is so close to 50, we will add 34+50. This is easier to solve. Then, since we added one extra to the original equation, we have to subtract one from the final answer.
To see a more detailed explanation of this strategy, and download some free printables to teach it, please see THIS POST.

NEXT STEPS:
Ready to get really strategic with your approach to teaching math facts?
- Implement The Addition Station – a self-paced, student-centered program for the basic addition facts and strategies (see Grades 1-2 HERE and Grades 3-4 HERE).
- Try out Addition Strategies Task Cards as a way for your students to practice each addition strategy in isolation. See the full bundle for 1st Grade, 2nd grade, 3rd grade, or 4th grade.



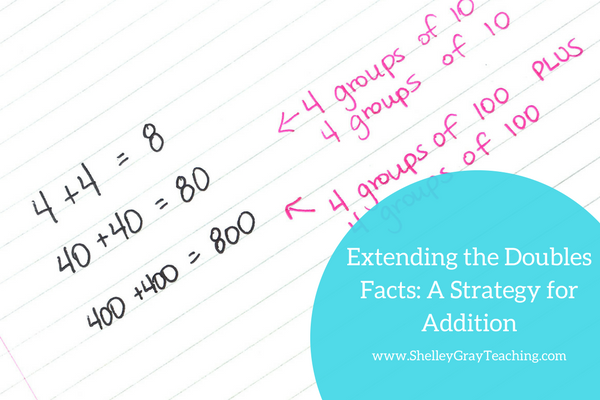

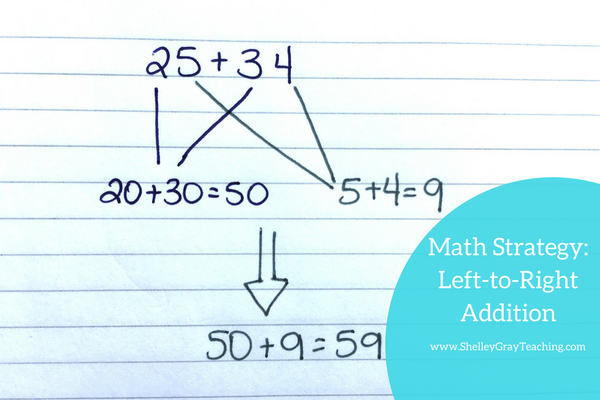








4 Comments
I’m a first year trainee primary teacher and this has helped me massively to find out the basic strategies to help me further my learning.
I am going to pass this on to my fellow class mates
An excellent post clearly explaining the strategies. Thank you it will help me plan lessons and centers 🙂
very simple and well-explained strategies that can be taught student teachers.