Number Talks have gained in popularity over the last several years – and for good reason! They are a powerful and collaborative way for students to use mental math and to see how math is flexible. Often math is seen as being either right or wrong. But number talks help students see that there is no one right way to solve a problem, and they can use strategies that make sense to them. If you’re thinking of changing up your regular Number of the Day routine for a Number Talk routine, here’s all the information you will need!

What are Number Talks?
Number Talks are short, 5-15 minute whole-class discussions with a goal of building number sense. The focus of the discussion is on all the many ways to solve the problem, rather than on the answer itself. During a number talk, the teacher poses a problem and students share strategies, reflect on others’ strategies, and learn to see math in different ways.
For example, let’s suppose the teacher presents 10+12 and asks students to solve it. There are so many ways to solve 10+12! One student might see this as the double of 10 plus 2 more. Another might imagine ten frame images. Another might think about the double of 12 and then subtract 2. As students share their thinking and the teacher writes it down, other students are exposed to new ways to think about this problem. This is a fantastic time to reinforce mental math strategies that you have taught such as doubles, near doubles, counting on, making ten, etc.

The Benefits of Number Talks
It’s easy to see the benefit of number talks.
- Number talks require very little (to no) prep time.
- They encourage students to be flexible with numbers (one of the big goals of fact fluency!).
- They foster a safe space for making mistakes.
- They allow students to explore important connections and relationships.
- They give teachers a chance to identify misconceptions.
- They allow students to consider strategies that they may not be familiar with.
How to Do a Number Talk
Any way that you can get your students talking about numbers and strategies will benefit them! But here is a typical routine for number talks:
- Pose a problem.
- Allow thinking time. When a student has a strategy, he puts a thumb to his chest. If he thinks of additional strategies, he puts a finger up for each one. This encourages students to keep thinking of new strategies rather than sitting mindlessly after they’ve got one.
- Ask for answers. Record them on the board without judging them as right or wrong.
- Ask for a volunteer to defend an answer.
- The volunteer explains his strategy.
- Teacher records thinking.
Let’s take a look at what a number talk might look like in a 5th grade classroom.
The teacher poses the problem 22×5 and allows all students thinking time. As students think of strategies, they put a thumb to their chest and a finger up for each additional one. This ensures that other students aren’t distracted by hands shooting in the air as students think of a strategy.

The teacher asks for answers. As students volunteer their answers, the teacher writes them all on the board – without judging them as right or wrong.

The teacher then asks for a volunteer to defend an answer. One student says, “I agree with 110. I know that 22 is 20 and 2. 20×5 is 100, and 2×5 is 10, so the answer is 110.” As the volunteers explain their answers, the teacher records the thinking on the board. This step helps other students understand the strategies and see each other’s thought processes.
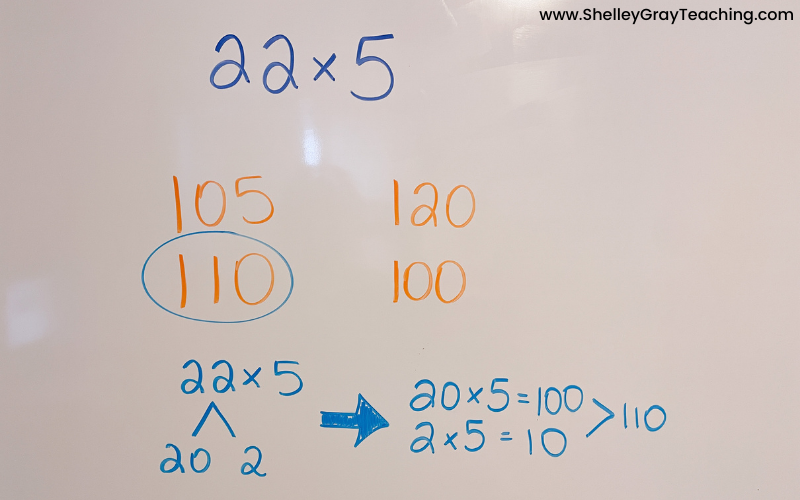
Since there is more time remaining, the teacher asks for other volunteers to defend an answer. Another student says, “I agree with 110 too, but I thought about it differently. I imagined 22×10, which I knew was 220 and then I divided it in half since we were multiplying by 5 and not 10.”
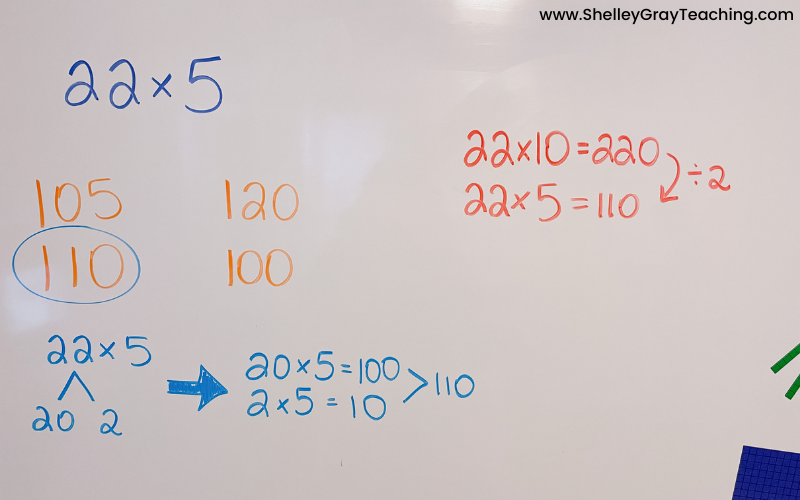
At this point, the student who volunteered the answer 105 says, “I want to change my answer to 110 too. I see where I went wrong when I was thinking about it before.” The teacher asks the student to clarify her mistake and praises her because mistakes are celebrated! The teacher says, “I can see why you made that mistake! You were thinking of 20 groups of 5 and then ONE more group of 5 instead of two. “
A third volunteer says, “I also agree with 110. I imagined an area model where I did 10×5, 10×5, and 2×5. I got 110.”
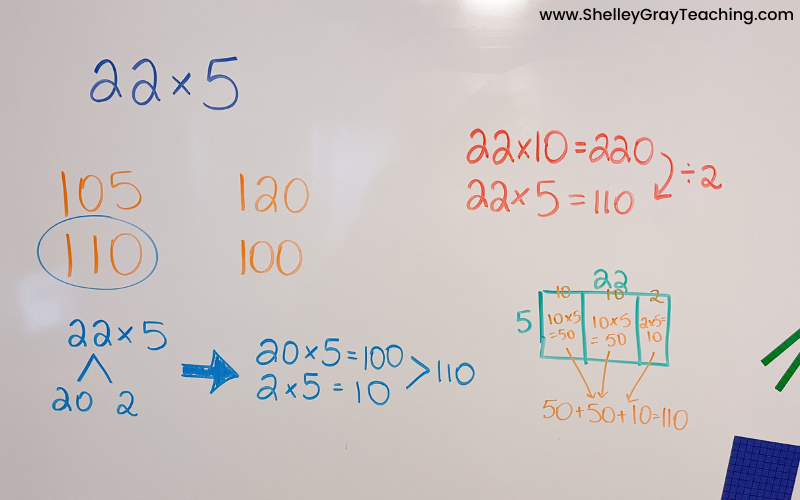
The class then comes to the conclusion that 110 is the correct answer for this problem.
As you can see, the number talk process is powerful. This quote from Making Number Talks Matter by Cathy Humphreys and Ruth Parker sums it up beautifully.
“When you shift away from teaching ‘what to do,’ encouraging students to think in their own ways; away from teaching procedures for students to practice to posing problems and letting students grapple with them; and away from knowing what you want students to say to listening with honest curiosity to the things they have to say, then your teaching and life in your classroom will be forever changed.” – Making Number Talks Matter by Cathy Humphreys and Ruth Parker

Alternative to the Traditional Routine: How Did You Solve It?
Some teachers find that a different process fits their classroom better. If you would rather not do the exact number talk practice as outlined above, try a simple strategy sharing session. In this type of number talk, a teacher might say, “Let’s think about all the different ways we can solve 22×5.” Allow thinking time, and then ask for volunteers to share their strategies. Make this a challenge to see how many different strategies students can come up with!
This routine can be made even more powerful by having students take time to reflect on others’ strategies. Have students use sentence starters like the ones below:
- I agree/disagree with ________________ because…
- I like/don’t like that strategy because…
- _______________’s strategy makes sense to me because…
- I know this strategy works because…
- Something I’m not sure about is…
- Something I notice is…
- I’m wondering if…
- I see it in a different way. Here is how I’m thinking…

Math Conversations: An Alternative to Consider
Traditionally, number talks involve mental math skills. But we can expand number talks to more of a “math conversation” where we talk about and share strategies for any math topic and solve a wide range of problems! Let’s take a look at some examples of math conversations you can have in your classroom.
Here’s an example of an open-ended task where students focus on finding as many answers as possible. When students share their answers, they justify them.

In this next example, students focus on fractions. Again, the focus here is on many different answers. One student might see this as 8 groups of one-fourth. Another might see it as 8 groups of three-fourths and two wholes. This can then be extended to a conversation about how this image is seen. We could see it as one and one-fourth on top, and three-fourths on the bottom to make 2. There are many different options. This is a fantastic way to make fractions more conceptual.

In this example, we are using subitizing in a way that encourages multiplicative reasoning. The conversation here can be focused on how we see the images. Do we see groups of 7? Groups of 14? 21, 7, and 14 more covered up? Maybe a student sees 21 on top and 21 on the bottom. This makes for engaging conversation.
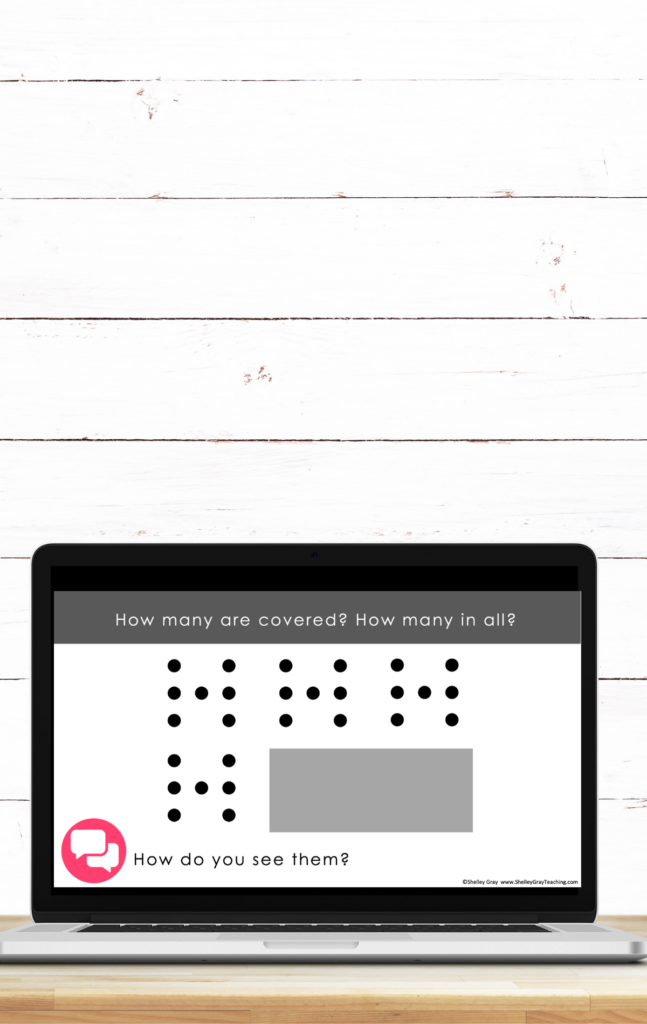
This next example comes back to mental math, but here we are giving students two estimation strategies and asking them to reflect on them. A good extension would be to ask students if they can think of some useful strategies for solving this problem.

Here’s another example of how we can incorporate fractions into math conversations in an open-ended way. There are many different possible answers, and this can even be extended to improper fractions. The important part is that students justify their answers and explain their thinking.

Thing to Remember
As you implement a new number talk routine, here are some things to remember:
- Number talks might feel uncomfortable at first – for both you and your students.
- Listen, rather than tell.
- The more consistent you are, the better results you will get!
- It may take time for students to feel comfortable sharing.
- Don’t call on students, but let them volunteer instead. You want them to use their mental space for strategizing, not for worrying about being called on.
- It may take time for students to get used to the “struggle” of thinking during number talks. Encourage this struggle!
Related: Ten Things to Include in Your Number of the Day Routine
Getting Started With Number Talks
If you’re still reading this, you’re probably excited about implementing a number talk routine in your class and eager to get started! But the thought of a new daily routine can be overwhelming. Remember that you will need to start slowly and work your way up to some of the number talks that have been covered here. To get your students used to talking about math (and being comfortable doing it) here are some easy ways to get started:
- Double a number: Write a number on the board. Ask students to double it and share how they did it. They will have many different strategies! For example, to double 350, some students might think 300+300+50+50. Others might imagine a number line where they start at 350, then add 50 more, then 300 more. Hearing students’ thought processes can be fascinating!
- Halve a number (use the same process as above for doubling).
- Get to the next ten. Write a number such as 342 and ask students how they would think about getting to the next ten. Then try getting to the next hundred. How does their thinking change?
- Subitize with dot images. Have students share how they see the dot images. There are many different ways to see them!
Once your students get comfortable with talking about math, they will be ready to get onto some more advanced number talks!
Time-Saving Math Conversations
If you are interested in starting a math conversations routine using ideas like the ones I shared above, you might be interested in these Math Conversations slides. They are completely ready to go! Just choose one for the day and your prep is complete! Each package includes 200 Math Conversations prompts so you have plenty of options for your class. Direct links are below.
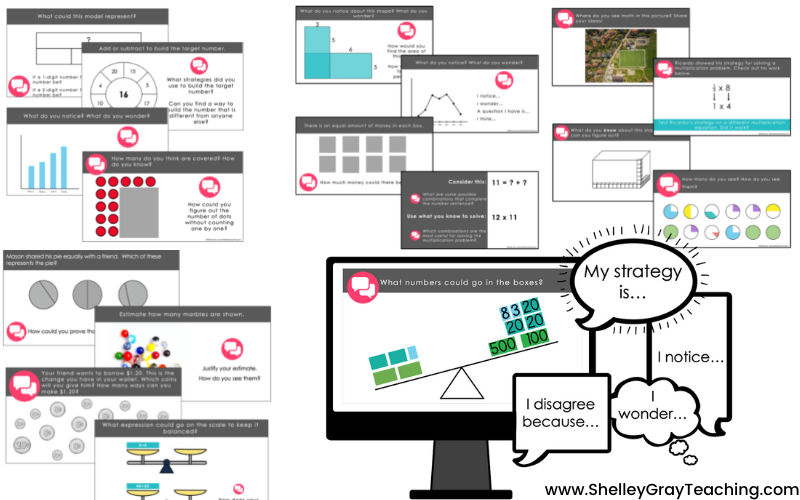
- Math Conversations for First Grade
- Math Conversations for Second Grade
- Math Conversations for Third Grade
- Math Conversations for Fourth Grade
- Math Conversations for Fifth Grade
Here’s what some teachers are saying about Math Conversations:
“These are an amazing way to start our math block. Very engaging and students love that there is more than one answer. I love seeing all the different ways my students reflect on the questions being asked.” – Jennifer
“I absolutely love this resource!! What amazing mathematical conversations were sparked with the slides. My mathematicians loved sharing their ideas and encouraging others to share as well. This resource is a great fit for a morning activity to wake up our math brains or to conclude a math class. Excellent resource.” – Christina
“I am using this in my small group math stations. My students had a hard time with the fact that there isn’t one specific answer I’m looking for, but they are starting to get the hang of it! I love seeing all the different strategies they use to solve the problems, and I’ve noticed that it’s getting easier for them to explain their thinking!” – Rebecca
If you’d like to see more math conversation slides before purchasing, I’ve put together a free sample that I’d be happy to send right to your inbox. Just sign up here, and it will arrive within minutes.
Good luck with your classroom number talks!







2 Comments
Hi Shelley,
Stumbled across your website, via a friend’s post on Facebook.
Although I’m enjoying the Christmas/New Year holidays, I’m already thinking about the 2022 school year and I am very impressed with your visual ‘Maths Conversations’ but I have a question – I’m going to have a 3/4 composite class this year – would you suggest I go with the Year 3 Maths Conversation kit or the Year 4 kit as a first purchase?
Kind regards,
David
Hi David! If you are only going to purchase one package, I’d recommend the lower grade one – so 3rd Grade in your case. The conversations will still be invaluable and you can always provide enrichment by discussing what would happen if…(you used a higher number/you used a fraction/etc). Hope this is helpful!
Shelley