Fractions can be a difficult concept to teach. Often we get very focused on fractions as a part of a whole or part of a set, and teach fractions mostly as parts of a pizza, parts of a pie, etc. Fractions are more than parts of a pizza. Our students must be able to think deeply and conceptually about fractions. Students should understand fractions as numbers that come between specific whole numbers. For example, there are other numbers that come between 0 and 1, such as one-fourth, one-half, or two-thirds.
So how do we effectively teach this? We use a number line.
A number line is an important tool that should be used frequently throughout your fractions unit.
Some advantages of using a number line to teach fractions include:
- Number lines help students see fractions as not only parts of a whole or parts or parts of a set, but as a part of distance or a part of time.
- Number lines help us compare fractions.
- Number lines help us find equivalent fractions.
- Number lines help us see a fraction as a number that comes between two whole numbers.
- Number lines are an effective alternative to traditional visual models that we use to teach fractions.
How do we teach fractions on a number line?
Below I have included a full lesson plan for teaching fractions on a number line. This is intended as an introductory lesson for this concept. I have also included a printable version of this lesson plan for you. Download it HERE.
LESSON PLAN – INTRODUCING FRACTIONS ON A NUMBER LINE
Overview:
In this lesson students will be introduced to the idea of fractions on a number line. This lesson only uses halves, thirds, and fourths as a starting point for this concept.
Objective:
- Students will see fractions as numbers on a number line.
- Students will represent fractions on a number line.
- Students will use a number line to solve basic problems involving fractions.
Materials:
- Fraction bars (one copy for each student) and Fractions on a Number Line activity sheets – Download HERE.
- Sticky notes (one for each student)
- *Optional for Extension* Fractions on a Number Line Task Cards – Find them HERE.
Activating Prior Knowledge – Spend a few minutes reviewing what students already know (3 minutes).
By this time you have spent time teaching students about fractions as part of a whole or part of a set. Review this concept:
- Show students a rectangular piece of paper. Say, “We have worked with fractions as part of a whole. Here I have one whole piece of paper. If I cut this piece of paper in half, what does each piece represent?” Cut the paper in half. Students should identify that each piece represents one-half of the whole.
- Say, “What if I cut each piece in half again?” Cut each half in half again so that you have four pieces. Ask, “Now what fraction of the whole does each piece represent?” Students should identify that each piece represents one-fourth.

Acquiring New Knowledge – In this part of the lesson our students will acquire new knowledge. Let’s help them see the number line as a tool to use with fractions. (8 minutes)
- Say, “We know that we can divide any whole into parts. But what if we want to divide something into parts that we can’t touch? What about dividing one hour into parts? How could we represent one hour?” Let students come up with ways to represent one hour. Write their responses down on the whiteboard. Guide them towards using a horizontal line to represent one hour. You may have to ask, “What about a line? Could we use a line to represent one hour?”
- Write a large horizontal line on the whiteboard. Make one mark at the beginning and one mark at the end. Ask your students, “If this entire line represents one hour, what should I write beside these notches?” Guide students toward answering “0” for the line at the beginning and “1” for the line at the end.

- Say, “Suppose that we play soccer for the first half of the hour, and then we play baseball for the last half of the hour. How could we represent that on this line?” Help students see that we could divide the line in half as shown below.

- Ask, “If we wanted to write the fraction “one-half” on this number line, where would we write it?” Students should be able to identify that if we wanted to write one-half, we would write it at the middle point as shown below.
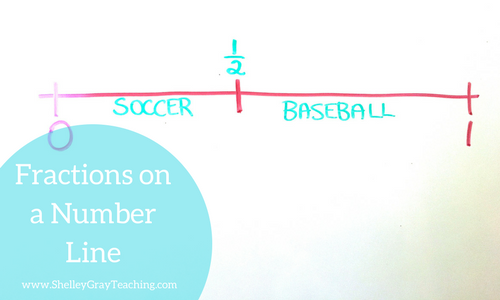
- Explain that each half of the number line represents one-half of the hour.
- Do another example using fourths of an hour. Have the students generate the ideas for how the hour could be divided into fourths.
NEXT EXAMPLE – Let’s try another example with distance rather than time.
- Say, “Let’s suppose that we want to divide one kilometer into parts. Could we use a number line to represent one kilometer?” Guide students toward the idea that we can use a similar number line, with 0 at one end and 1 at the other to represent one whole kilometer.

- “Let’s suppose that there is a girl named Lucy who is running one kilometer. So far she has run one-half of a kilometer. How could we show the distance that she has run on the number line?” Students should identify that we can divide the number line in half and show Lucy at the one-half point.

- “What if Lucy has run two-thirds of the kilometer? How could we show that?” Guide students toward the idea that we can divide the number line into three equal parts and show Lucy at the two-thirds point.

- As a class, do another example using fourths of a kilometer. Have the students generate the ideas for how the hour could be divided into fourths.
Guided Practice – In this part of the lesson students will work with fraction bars to enhance their understanding. (25 minutes)
- Give each student a set of fraction bars and the number line activity sheets.

- Work together to label the fraction pieces on the fraction bar sheet. Have students carefully cut out their fraction bars.
- Have students work with a partner to complete their activity sheets. As they work, circulate the room and ask questions to check for understanding. Your questions might start with:
- “How do you know that …”
- “What if…”
- “How can you tell if…”
- “What do these pieces represent?”
- Circulating the room as students work will also serve as your assessment of this lesson. This will help to drive your future instruction. Do your students understand this concept? Are they ready to move on to the next part of fractions on a number line? Is re-teaching required? Do you need to work with small groups on any of the concepts?
Wrap-Up – Let’s consolidate learning and reinforce the fact that fractions are numbers that can be represented on a number line. (3 minutes)
- Draw a giant number line on the whiteboard. Label it with 0 and 1.
- Hand a sticky note to each student. Ask students to write a fraction between 0 and 1 on their sticky note.
- In groups, have students approach the board and place the sticky note on the number line where they think it should go.
- This is another opportunity to check for any misunderstandings.

I’ve made this entire lesson plan available to you in a PDF version. If you haven’t already done so, download it here.
FOLLOW UP
These task cards for Fractions on a Number Line are a great way to reinforce this skill in a variety of different ways in order to maximize understanding. Get them HERE.
NEXT STEPS
Now that students have been introduced to the concept of fractions on a number line, we can keep reinforcing this concept. In upcoming lessons, be sure to focus on the following concepts:
- ordering fractions on a number line
- comparing fractions on a number line
- finding equivalent fractions using number lines
- problem solving with fractions using a number line
- relating number lines to other visual models (example: representing a fraction as a part of a whole circle, and as a part of a set, and on a number line)
If this all feels overwhelming to you, and you would like the planning done for you, you’ll want to check out The Fraction Station. This is a self-paced, student-centered approach to teaching fractions. Students work at their own pace to complete the levels, each of which includes independent activity sheets and hands-on activities. Check out the third and fourth grade fraction stations here.








4 Comments
I’m teaching fractions next week to a group of middle school self-contained special education students. I may have to teach the same objective for a while before some of my students will begin to grasp the concept. I was searching for different approaches to teaching fractions. I found that, a follow up lesson plan, and a new teacher to follow on TPT! Thanks!
So many times we only teach part of a whole. The students just cannot get past half a pizza! I am definitely implementing this in my classroom in the next couple weeks. In addition, I thought I would make a wall number line with string and clothespins for them to place a daily fraction or more to continue the idea for a few days longer. Thank you so much!
What a great and very thorough lesson plan. I love the practical side of this lesson. Thank you so much for sharing.