The halving and doubling strategy for multiplication is one of the most fascinating multiplication strategies. The best part is that it actually IS a strategy – not a trick.
First, let’s take a look at the halving and doubling strategy in action.
To use halving and doubling, you simply half one of the factors and double the other. Take this example. To solve 25×16, we could double the 25 to make 50 and then half the 16 to make 8. Suddenly this problem becomes much easier to solve!
We could actually take this one step further if we wanted to, by doubling the 50 to make 100 and halving the 8 to make 4. Now we are left with 100×4. So, the product of 25 and 16 is 400.
CONCEPTUAL UNDERSTANDING
It’s essential to know WHY strategies work. Let’s take a look at exactly why the halving and doubling strategy works. It’s easiest to see this in an array.
Here we have a 4×5 array.
Suppose we divide the number of rows in half and we rearrange them like this:
Do we still have the same number of objects? Yes! They are just arranged differently. Now we have a 2×10 array. All we did was half the number of rows and double the number of objects in each row.
Try this yourself with 3×8!
DOES IT ALWAYS WORK?
Halving and doubling will always work, but there are some situations that are better suited to it than others. For example, suppose you have 17×15. Technically we could half the 17 to make 8.5 and double the 15 to make 30. However, this does not make the problem easier to solve, and there are other strategies that would be more effective in solving 17×15.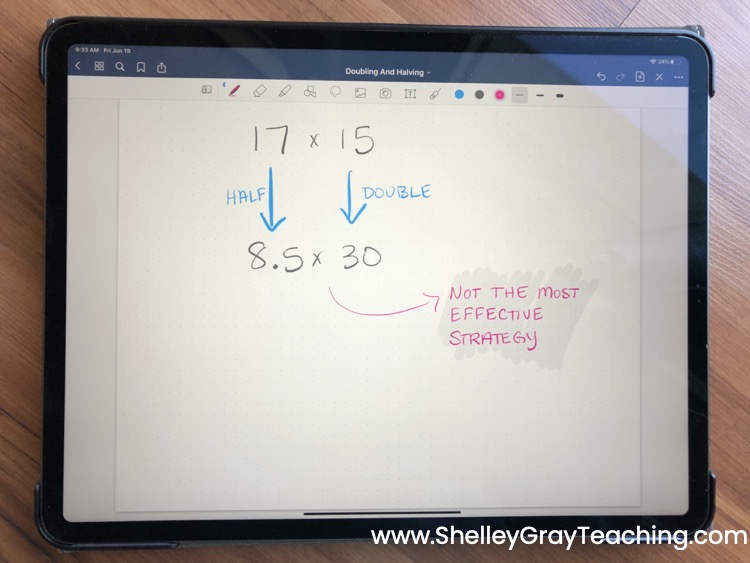
USING DOUBLING AND HALVING
Doubling and halving works best when one of the factors is even, and when the other factor is a number like 5, 10, 25, or 50. For example, doubling and halving would be an efficient strategy for:
- 50×18
- 120×5
- 25×20
TEACHING DOUBLING AND HALVING
Doubling and halving is a fantastic strategy for your students to work with. You can begin modeling doubling and halving with basic facts like 5×6. However, your students must understand WHY it works. It is not enough to simply tell your students that they can double one factor and half the other. The ability to visualize is key to conceptual understanding. This will be best done with arrays, so be sure to include lots of array practice as students build their understanding of this strategy.
Here are some other considerations to make as you teach doubling and halving:
- Allow students to discover this strategy on their own through activities with arrays. You might have students build a 5×6 array, and then a 10×3 array and ask, “What do you notice?” Then build a 4×7 array and a 2×14 array and ask the same question. Encourage students to look for relationships and connections.
- Implement math investigations where you ask pairs of students to investigate questions like:
-
- Do doubling and halving always work? Prove it!
- For which types of problems does doubling and halving work best?
- What kinds of problems are NOT very well suited to doubling and halving?
RESOURCES TO HELP
See this blog post in video format here.
This next video is intended for upper elementary students and explains the doubling and halving strategy. This can be used as an introduction.










