
Multi-digit multiplication is a difficult concept to teach. Long gone are the days where we teach one method, such as long multiplication, and just *hope* that all of our students catch on and can use that method effectively. Today we know the importance of teaching multi-digit multiplication more strategically. This ensures that every student in your classroom can experience success in some way. It also ensures that students’ knowledge is built on strategically, and that they really UNDERSTAND the process of multi-digit multiplication.
Alternatively, if you are looking for a resource where all of the work is done for you, you may be interested in this Multi-Digit Multiplication Station, where students work through a variety of strategies at their own pace, mastering each one as they go. Strategies are integrated in a strategic manner, ensuring that students build on their understanding progressively. See the Multi-Digit Multiplication Station HERE.
So how should you begin teaching multi-digit multiplication?
It’s important to start with strategies that will help students solve multi-digit equations mentally. Rather than jumping right into long multiplication or an effective alternative, begin with the following:
1. The commutative and associative properties. First of all, it’s important for students to remember these properties. The commutative property states that the order of the factors does not change the product. For example, 4×3 and 3×4 both equal 12. The associative property states that the factors can be grouped in different ways. For example, (7×2)x5 gives you the same product as (2×5)x7. These properties help students understand that they can manipulate equations to solve them easier.
2. Using Factors. This is a great way to teach students that numbers can be manipulated in order to make an equation easier to solve. When we teach multi-digit multiplication, our goal is not always to get a correct answer as quickly as possible. Sometimes our goal is to be able to think creatively when it comes to number. This is one of those instances. We could take the equation 4×15, and break the 15 into its factors, 3 and 5. Now we have this equation: 4x3x5. Now we could solve it like this: (4×3)x5 -> 12×5 ->60. This is just to show that there is not only one right way to solve this equation.
3. Multiplying by 10, 100, and 1000, as well as multiples of 10, 100, and 1000. Although I’ve grouped these two concepts together for the purposes of this blog post, this should be taught slowly and carefully, piece by piece. When you teach this concept, it’s important to focus on the place value rules before teaching tricks like the “adding zeros” trick. For example, when students are faced with the equation 45×100, they need to understand that the place values increase by 2 places, to make the product 4500. Similarly, when multiplying an equation like 3×1000, the place values increase by 3 places to make 3000. After students have mastered this concept, we can teach them that when there are 2 zeros in the factors, we add 2 zeros to the product. Keep in mind that these tricks should only be taught AFTER students possess an excellent understanding of the math behind the concept.
4. Breaking Up Numbers. This is one of the most useful mental math strategies out there. It involves breaking up one of the factors, multiplying in groups, and then adding those groups together. Here’s an example: In this example we break up the 12 into a 10 and a 2, and then multiply it in parts. So 12×30 becomes (10×30) + (2×30). This is much easier to solve!
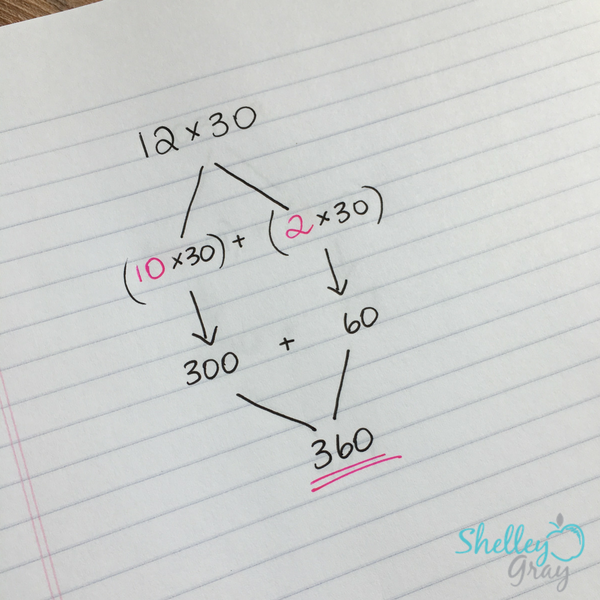
We can also use this strategy to multiply bigger numbers, like 103×9. We can break the 103 up into a 100 and a 3, and then multiply in parts, like this: (100×9) + (3×9).
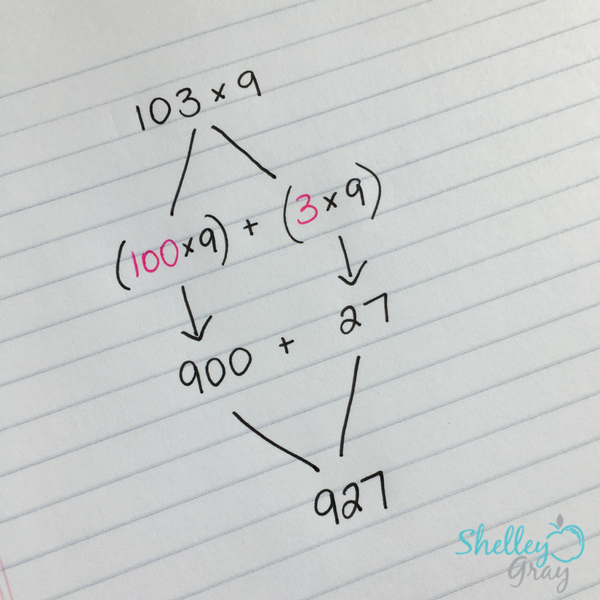
5. The Box/Window Method. I love the box/window method because it utilizes the expanded form of each factor, making this a great strategy to reinforce number sense concepts. To use this strategy, we draw a box (the number of columns and rows depend on the number of digits in the factors), and then write the expanded forms of the factors along the top and the side. Then we multiply each part, and add the parts together when we are finished. If you’d like a more detailed tutorial for this strategy, please see THIS blog post, which also includes a video tutorial.
6. Partial Products. This is one of the most important strategies to teach as an alternative to long multiplication. In partial products, the equation is set up like in traditional long multiplication, but the way we multiply is different. For example, for the equation 35×3, we first multiply 3×5 to make 15. Then we multiply 3×30 to make 90. Notice that we multiplied by THIRTY, not three. This is because that 3 represents 30. This gives us 90. Now we add the 15 and 90 together to make 105. If you’d like a more detailed tutorial for this strategy, please see THIS blog post, which also includes a video tutorial.
The strategies that I’ve outlined above are the MOST important ones for teaching multi-digit multiplication. All of these strategies place an emphasis on number sense understanding and ensure that students really understand what the numbers in each equation mean. But what about strategies like traditional long multiplication?
This is a controversial topic. Some teachers believe that our teaching should be ONLY number sense focused, so that we don’t teach strategies that don’t focus on number sense understanding. These teachers tend to use strategies like partial products all year long as a very effective alternative to traditional long multiplication. Other teachers believe that we should teach the way that multiplication was taught years ago. It worked then, so why wouldn’t it work now?! These teachers tend to focus more on strategies like traditional long multiplication, and less on more current methods like box/window or partial products.
I’m not here to tell you which way is better 🙂 This depends on you and your students. However, I will tell you my personal belief. Personally I tend to not go to either extreme. I am a huge believer in strategies that promote number sense understanding. However I also believe that there is a place for traditional methods for SOME of your students. You will have to be the judge here. If you have students who are struggling with multi-digit multiplication, you’ll probably choose to let them focus on partial products and box/window and leave it at that. Why add more confusion? They can be very successful with those strategies. HOWEVER, you might have some students who have an excellent number sense understanding of what you have taught so far, and are ready for more of a challenge! These students might thrive with other, less number-sense focused methods, since they already have a strong grasp of math concepts. For these students, I am going to talk about a couple of other strategies.
These next strategies are less number-sense focused, but they can be a fun way to multiply for those students who are ready for a challenge.
- Lattice Multiplication. This is a really fun method that involves drawing a grid and using that grid to organize the numbers. Some teachers find that carrying is easier for students using this method, because the numbers are arranged in diagonal rows, so it’s easier to see where they need to be added. This strategy takes awhile to explain, so please view THIS blog post, which also includes a video tutorial of the strategy.
- Halving and Doubling. This is a really neat strategy when multiplying by numbers like 5, 10, 25, 50, etc. All you do is divide one factor in half, and double the other one in order to change the equation, making it easier to solve. For example, if we have an equation like 25×14, we could double the 25 to make 50, and divide the 14 in half to make 7. Now we have 50×7, which is MUCH easier to solve! We can calculate this mentally, very quickly, and get our product of 350. For this strategy, students must understand that it only works well with certain numbers, and they’ll need plenty of practice with knowing which equations it works well with.
- Traditional Long Multiplication. This brings us to traditional long multiplication. I’m not going to explain how to do this, because I think most of us already know, but this can be taught to students who are ready for an additional challenge.











11 Comments
I wish I studied math with you then I wouldn’t have struggled as I did. Anyway I will share this with my children.
Thank you. I have always wanted to know how to do lattice math now I know.
A friend tried to explain the lattice method without much luck…I’ve just practised it several times and now feel confident that I can introduce it to my Grade 4/5 class later this month! SO COOL and exciting!
Hi there i am a new homeschooling mom, to a very bright 8 year old daughter. I just have to say your ways of teaching multi- digit math are amazing. they are so simple to fallow and strait forward. my daughter watched your video on lattice method and on the window method and with in 25 min shes got both down. thank you so much for putting out these videos and we hope to see more of your work soon
That’s fantastic, Cristal! Thank you for sharing with me 🙂
Thank you for sharing, Shelley. This write-up is the best I’ve seen on the subject.
This is fantastic. Thank you for making this so clear. Do you teach on Outschool or any other platforms?
Hi Kiley! You’re very welcome! No I don’t – sorry! I’ve been planning on designing some courses for awhile now but they keep getting pushed down my to-do list!
The breaking up numbers method worked great for my cognitively impaired students! YAY!!