
Long division is often considered one of the most challenging topics to teach. Luckily, there are strategies that we can teach to make multi-digit division easier to understand and perform.
The Box Method, also referred to as the Area Model, is one of these strategies. It is a mental math based approach that will enhance number sense understanding. Students solve the equation by subtracting multiples until they get down to 0, or as close to 0 as possible.
If you plan on teaching the partial quotients strategy in your classroom (which I highly recommend) the Box Method is a great way to get started. It uses the same steps as partial quotients, but is organized a bit differently.
Let’s learn how to perform the Box Method/Area Model for long division!
Wait! Are you looking for the Area Model for multiplication rather than division? Find it HERE.
Below, I have included both a video tutorial and step-by-step instructions.
VIDEO TUTORIAL
AREA MODEL/BOX METHOD FOR LONG DIVISION: STEP-BY-STEP INSTRUCTIONS
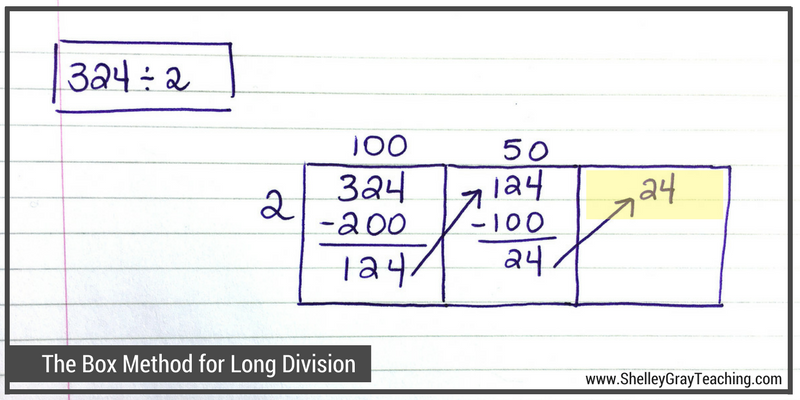
Suppose that we want to solve the equation 324÷2.
Step 1:
First we draw a box. We write the dividend inside the box, and the divisor on the left side.
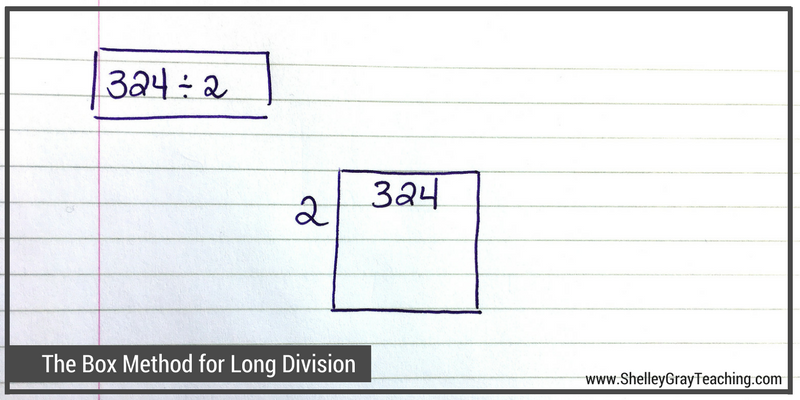
Step 2:
We want to figure out how many groups of 2 can be made from 324. We will do this in parts to make it easier. We could start by making 100 groups of 2, since we know that we have at least this many groups. So we multiply 100×2 to make 200, and then take that 200 away from 324. Now we have 124 left.
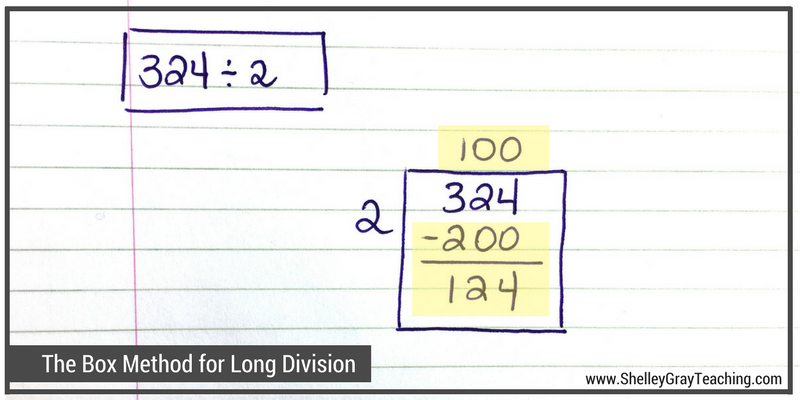
Step 3:
We make another box and carry the 124 over to it. Now let’s take away another easy multiply of 2. How about 50 groups of 2? We know that we can take out another 50 groups of 2 from 124. 50×2=100, so we take 100 from 124. Now we have 24 left.
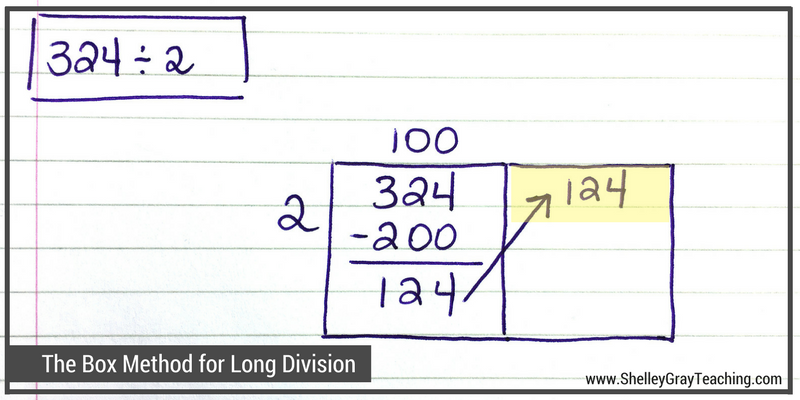
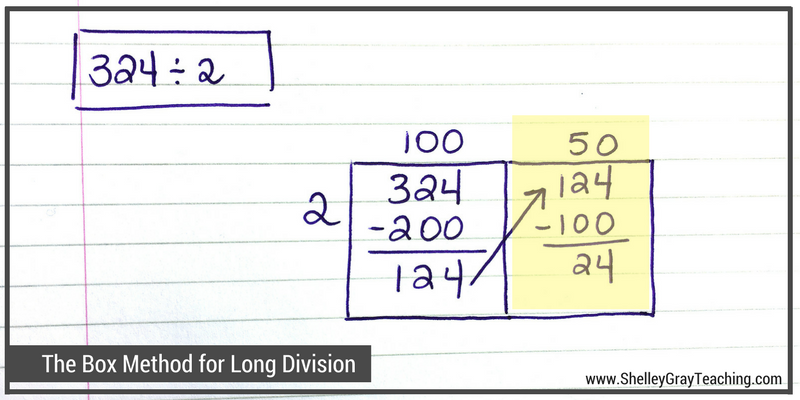
Step 4:
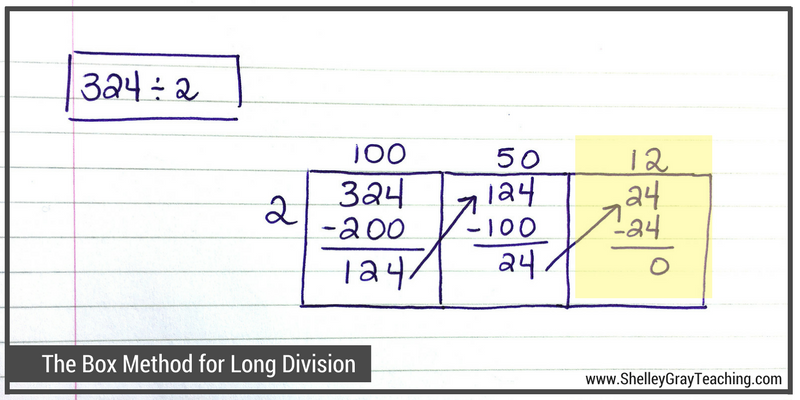
We make another box and carry the 24 over to it. We know that 12 groups of 2 makes 24, so let’s write a 12 on top and take away 24 from the 24. Now we end up with 0, so we know that we are finished our equation.
Step 5:
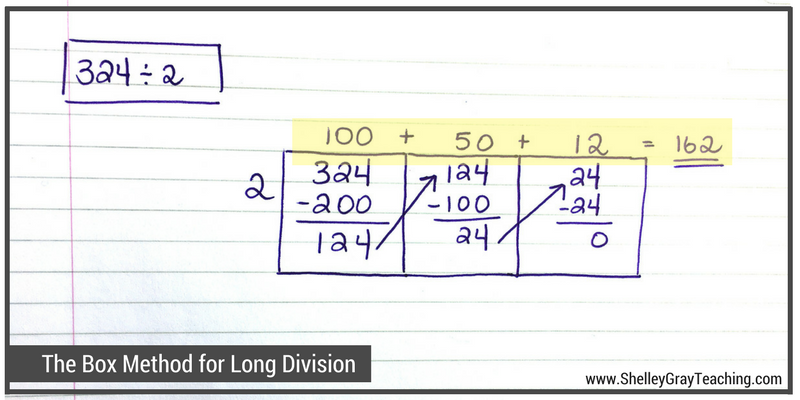
Now we add the “parts” from the top of the boxes to find our quotient. 100+50+12=162, so we know that 324÷2=162.
ONE MORE EXAMPLE (WITH A REMAINDER)
Let’s take a look at one more example. In this example, we will solve 453÷4.
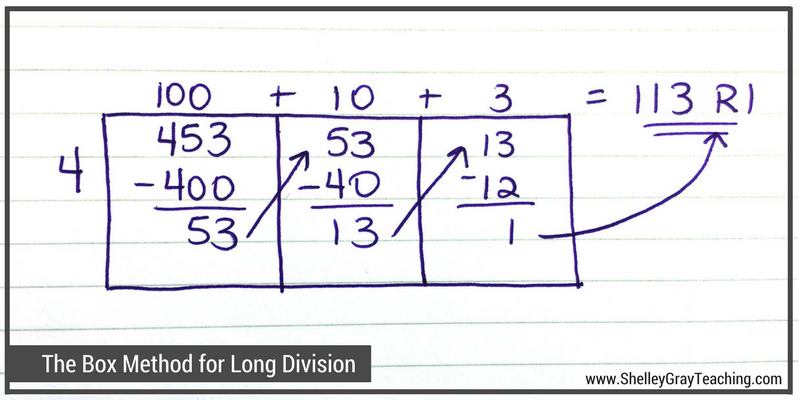
- First we wrote our dividend inside the box, and our divisor on the left side.
- We took out 100 groups of 4 first. This made 400. We subtracted 400 from 453 and were left with 53.
- We carried the 53 to the next box, and then took out another 10 groups of 4 to make 40. We took the 40 away from the 53 and were left with 13.
- We carried the 13 over to the next box, and then took out 3 groups of 4 to make 12. We took the 12 away from the 13 and were left with 1.
- We cannot take any more groups of 4 out, so our remainder is 1. To find our final quotient, we add 100+10+3+remainder 1 to make 113 R1.
The Area Model for Multiplication
The area model is fantastic for multiplication as well! If you’d like to read about how to teach this in a concrete way, here’s a post you may be interested in.

BOX STRATEGY/AREA MODEL TASK CARDS
These task cards give students the opportunity to practice the box method/area model for long division in a variety of different ways. Students will calculate quotients, solve division problems, figure out missing dividends and divisors, think about how to efficiently solve an equation using the box method, and more. See the Box Method Task Cards HERE or the Big Bundle of Long Division Task Cards HERE.
THE LONG DIVISION STATION
The Long Division Station is a self-paced, student-centered math station for long division. Students gradually learn a variety of strategies for long division, the box method being one of them. One of the greatest advantages to this Math Station is that is allows you to target every student and their unique abilities so that everyone is appropriately challenged. See The Long Division Station HERE.









7 Comments
Very well taught, understandable. Thanks.
Substitute gets it.
That is wonderful! My son uses the box method for multiplication , but becomes visually frustrated and angry when he was figuring out long division today. I have never seen this method before in my life. Totally makes sense. Thank you
love it so easy to work with