Lattice Multiplication: A Method for Multi-Digit Multiplication

 

Lattice multiplication is an alternative to traditional long multiplication. Before I begin explaining this strategy, I do want to take a second to talk about multi-digit multiplication strategies in general.

We know that number sense is an essential component of today’s classrooms. We teach math in a way that enhances number sense understanding, so that students really understand what they are doing, rather than just memorizing a series of steps.

Now let me begin this post on lattice multiplication by saying that this is not necessarily one of those strategies that enhances number sense understanding.

So why would you want to teach this strategy?

Once students have a solid understanding of the place value concepts behind multiplication, some can thrive with traditional methods such as long multiplication, or this alternative – lattice multiplication. I do believe that before you teach this method, you should focus on mental math strategies that DO encourage number sense understanding, such as the partial products strategy, or box/window method (area model). If your students have mastered those mental math based strategies, and are ready for more, this is a fun one to teach!

Looking for support with teaching this strategy and many others for multi-digit multiplication? See The Multi-Digit Multiplication Station (a self-paced, student-centered approach) HERE.

 

How do you perform lattice multiplication?

Lattice multiplication utilizes a grid to keep numbers organized. This is especially helpful when it comes to regrouping, as the numbers that are carried are also written within the grid to make the adding easier.

I’m going to explain this strategy step-by-step, with lots of pictures, but if you’d rather watch my Lattice Multiplication video, simply press “play” below! Otherwise keep scrolling for the step-by-step instructions.

Let’s begin with an equation that does not require regrouping: 18 x 31. To solve this equation, we follow the steps below:

Step 1: Draw a grid. The number of rows and columns will depend on the number of digits in the factors. For example, if you are multiplying a 2-digit by 2-digit equation, your grid will have two rows and two columns.

 

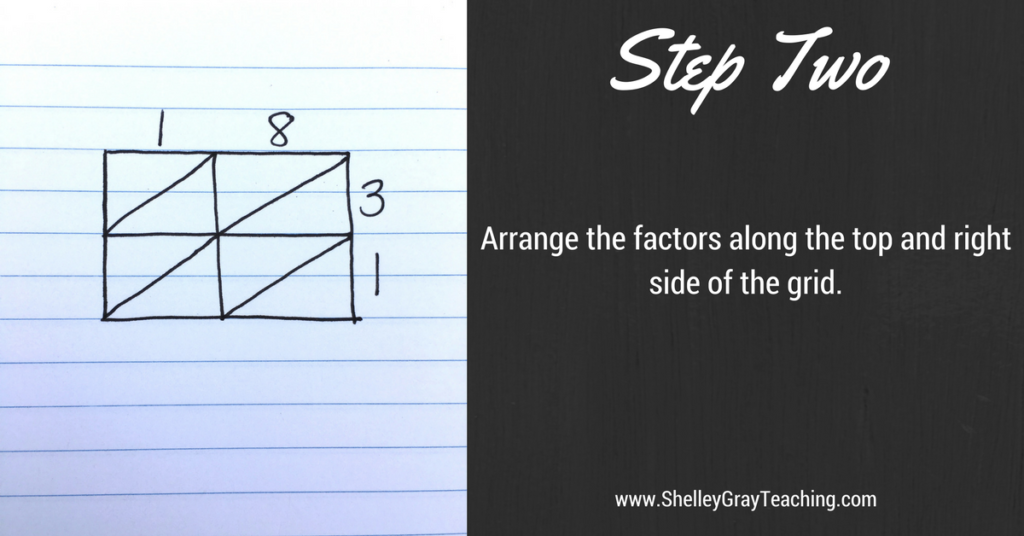
Step 2: Next, we arrange the factors along the top and right side of the grid, as shown below.

 

Step 3: Now it’s time to multiply. We multiply the numbers that meet in each space on the grid. For example, in the top right corner, we are multiplying 8×3 to make 24. The tens and ones are split on either side of the diagonal line.

 

Step 4: We continue multiplying for each space on the grid.

 

Step 5: Lastly, we add! We add using diagonal rows, and write the sum of each diagonal row along the left side and bottom of the grid. So in this example, the final product is 558.

 

Now what happens if we need to regroup? Let’s take a look below.

When we regroup, we simply carry the tens digit to the next diagonal row. In the example below, we have done all of our multiplying on the grid. Now when we add, let’s see what happens.

First we add the diagonal row in the bottom right, to make 0. (see example above)

Now we add the next diagonal row. The sum is 15, so here we write the ones digit (5), and carry the tens (1) to the next diagonal row (I’ve circled that carried digit in this example so that it stands out). Now, when we add that diagonal row, we simply add that carried digit in there as well.

This is often helpful for students because the carried digits stay in the row that they need to be added in, eliminating the confusion that carrying can often bring in traditional long multiplication.

 

What if we have more digits in the factors?

Easy!

We simply increase the numbers of rows or columns based on the number of digits in the factors. The example below shows a 2-digit by 3-digit equation, so there are 2 rows and 3 columns.

 

I do want to reinforce one more time that this is not a strategy that you would teach students who are just learning multi-digit multiplication. Please make sure you are focusing on mental math strategies that reinforce number sense first. THEN strategies like this one can be a fun addition to your multi-digit multiplication, and can really be helpful for some of your students.

 

NEXT STEPS:

 

Looking for more help with multi-digit multiplication in your classroom? Check out the self-paced, student-centered Multi-Digit Multiplication Station HERE.