
So you’re ready to implement mental math addition strategies this year, but aren’t sure where to start! All the different ways to teach addition facts can be overwhelming – counting on, doubles, left-to-right addition, breaking apart numbers, and so much more – how can you teach these mental math concepts strategically so that more of your students can develop addition and subtraction fact fluency?
Can’t we just teach our students to memorize?
The short answer is no, and my hope is that by the time you get to the end of this article you’ll see why mental math strategies are so essential to the overall math understanding of our students.
First, it’s important to understand the rationale behind mental math. Why is it important to teach these different strategies rather than simply teaching students to memorize the facts?
What is Mental Math?
So what does this mean? Let’s illustrate it with two different students – one who uses memorization, and another who has been exposed to mental math strategies.
STUDENT #1
This student is knows that 16+4=20 because she has practiced this fact over and over and over again.
When the teacher asks her to solve 16+5, she’s stumped. This is a fact she hasn’t learned yet.
After moving on to other math units and focusing less on addition, the fact 16+4 is forgotten and will have to be re-learned next year.
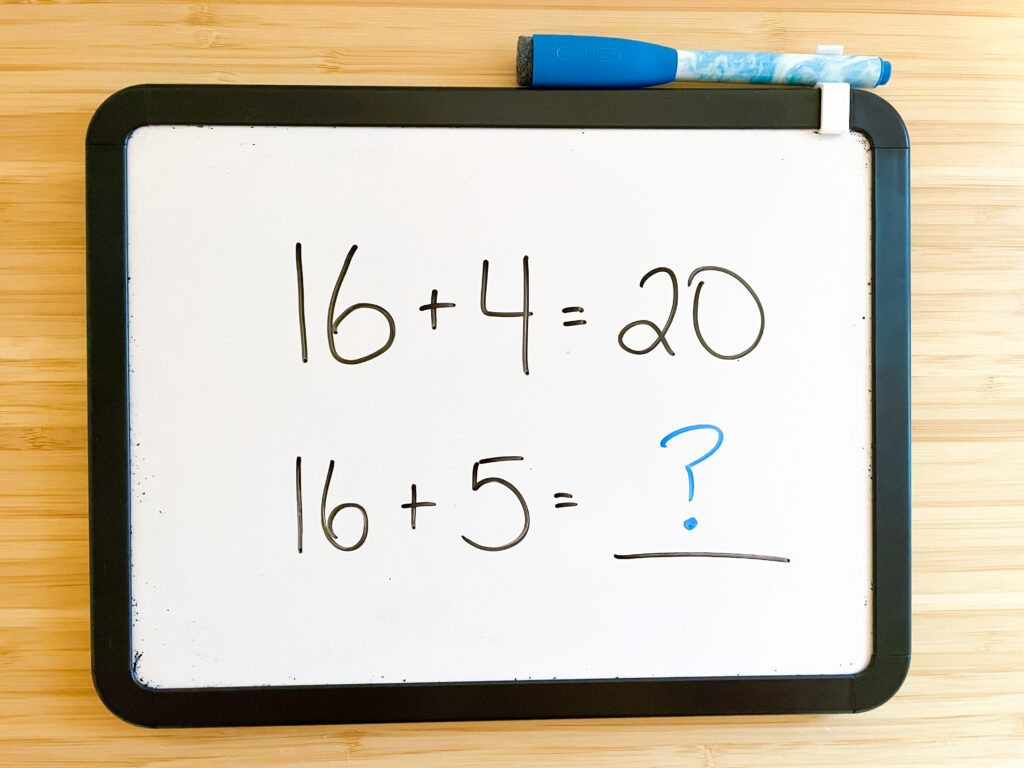
STUDENT #2
This next student hasn’t learned the fact 16+4 yet, but can easily figure it out because he knows that 6+4 is ten and then 10 more is 20.
When the teacher asks him to solve 16+5, he is easily able to visualize it because of all the work their class has done with ten frames. He already knows that 16+4=20, so 16+5 is just one more!
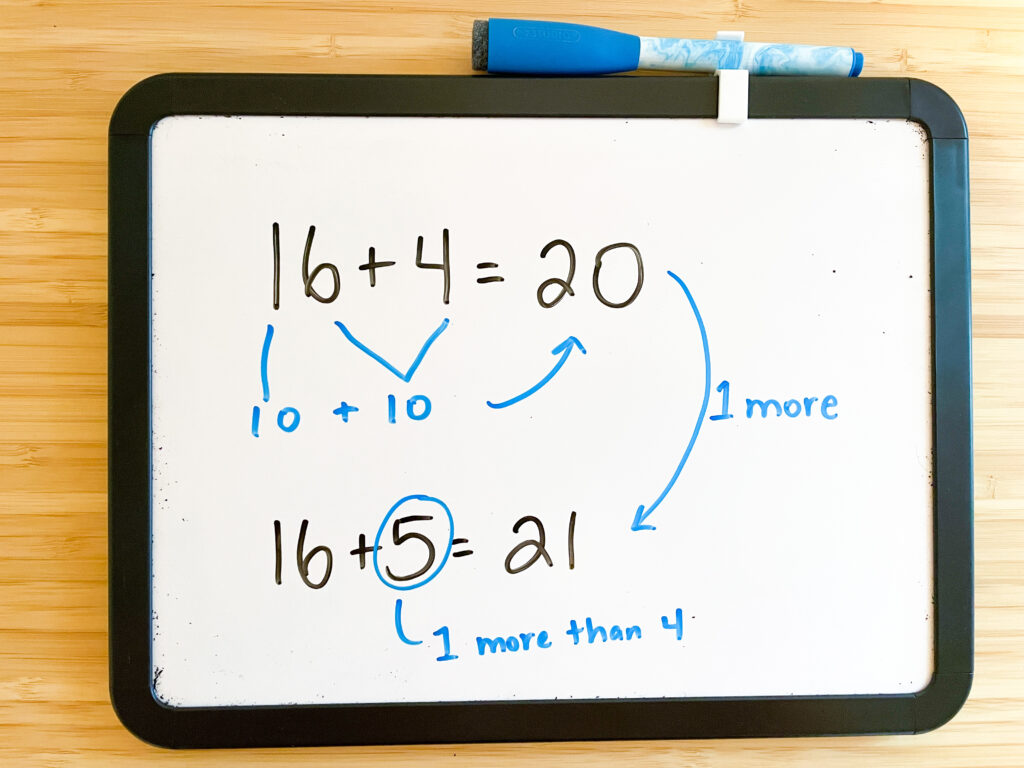
Then he thinks of one other way he could have solved it! He imagines the 16 as a 10 and a 6. He adds the 6 to the 5, which is a doubles plus one fact (11) and then adds on the remaining 10 to make 21.
Opponents of mental math will say this is too confusing, but I’ve simply written it all out so that you can see the steps that happen in a person’s head very quickly. This does not need to be written out like this every time.

This student has developed flexible thinking because of being exposed to mental math strategies. He will be able to use this exact same thinking to solve a problem like 126+15 in mere seconds.
The best part is that he has also developed confidence. He knows that he doesn’t have to rely on simply remembering the facts he’s been taught.
Instead, he possesses something much greater – understanding.
Understanding is a Gift
This might sound cheesy, but I wholeheartedly believe it. When you teach in a way that promotes real understanding, you are giving your students a gift.
It breaks my heart when I hear students say, “I’m not good at math because I’m not fast,” or “I can’t do math.”
The truth is that when math is taught mostly for memorization, there are SO MANY STUDENTS being left behind because they cannot grasp the content in that way. This can cause fear of math, math anxiety, and low confidence.
So what can we do?
Getting Started with Mental Math
There is no right answer to any of these questions. It will depend on your class, their unique needs, and their previous experience with mental math.
That being said, here are some of my top tips for getting started with teaching math strategies.
Step 1: Take on the Role of Facilitator Instead of Teacher
We can learn so much by simply listening to students. This is a mindset shift for many teachers because it feels different than what we’re used to! When you talk about math with your students, let them explain their thinking without jumping in to course correct them or reinforce the strategy that you used personally.
Step 2: Use Visuals and Manipulatives
If the thought of using manipulatives feels intimidating, just let kids explore with them for awhile. Ask questions like, “What are some different ways we could show 15+15 with these base ten blocks? Could we show it another way?”
You might just be amazed at what they come up with!
Step 3: Ask, “How else could we solve this?”
Try having an exploration session with different types of manipulatives like ten frames, base ten blocks, rekenreks, and cubes. Give students a problem to solve and challenge them to solve it in as many ways as possible. Have students share their thinking to introduce other students to alternative strategies and ways of thinking.
Step 4: Focus on Connections
If we know that 16+15=31, then we know that 26+15 is 10 more. This can be made visual by using base ten blocks.
26+15 is 41, then 126+15 is 100 more.
Rather than simply solving a problem and leaving it at that, try to connect it to something new. This is the concept behind number strings, which I will elaborate on in another post.
MENTAL MATH ADDITION AND SUBTRACTION STRATEGIES
Mental Math Strategies
Mental math strategies don’t necessarily have to be something that you explicitly teach. The goal in our classrooms should not necessarily be to “teach” the strategies, but rather to foster an environment where students construct their own understanding. We want to be careful that we don’t teach the strategies as pieces of information to memorize. Instead, we want students to be able to think flexibly when solving problems.
This being said, it can be useful to have a guide for some of the most useful strategies so that you have an idea of where you are heading.
That’s why I’ve done the research and broken it down into the seven most useful mental math addition strategies. These range from beginning strategies to more advanced, and will help your students develop true fact fluency. Read on to learn about each one!
Or, if you’d rather have all the work done for you, I’ve created extensive teaching resources for each of these strategies that include strategy posters, conceptual worksheets, station activities, math talks, and much more. See more about those units HERE.
THE ADDITION STRATEGIES
Counting On
Counting On is a beginning mental math strategy. When you count on, you start with the biggest number in an equation, and then count up. For example, to solve 5+3, you start with the “5” and then count up, “6, 7, 8.” This is to discourage students from counting like, “1, 2, 3, 4, 5…..6, 7, 8.” Students also need to understand the commutative property of addition, where if an expression looks like this: “2+6,” they still should start with the bigger number (in this case, 6) and count up “7, 8.”
Here’s a video to explain this strategy in more depth, or find a unit for teaching the counting on strategy HERE.
Doubles
The doubles are not necessarily a , but rather a set of facts that is easy to learn and remember. Doubles are all around us; think of fingers and toes – 5+5, wheels on a car – 2+2, or the eggs in a carton – 6+6. Building a strong foundation of doubles will help students with the next strategy, Doubles Plus One.
Near Doubles
This strategy is a natural progression from the doubles. It includes using a known fact and building on it. For example, to solve 6+7, a student could think, “I know that 6+6 makes 12, and one more makes 13.” This strategy is best modelled with ten frames, which makes it easy to see! Students need to SEE math so they can build their understanding!
Make a Ten
Make a Ten is a mental math strategy where students use the number combinations that make ten to form connections and relationships to other facts. First, students must learn the number combinations that make 10. Then they can confidently use those combinations. For example, to solve 8+5, a student might think, “I can take two from the 5 and give it to the 8 to make a ten, and then add the leftover 3 to make 13.” Ten frames are a fantastic way to illustrate this strategy.
Here’s a video that explains the make a ten strategy in more depth.
Find a unit for teaching make a ten HERE or find the math mats shown below HERE.
Making Multiples of Ten
This strategy is a natural follow-up to making ten. To make , we can use the number combinations that make ten (6+4, 7+3, etc.). This helps us recognize that expressions such as 26+4 will make a multiple of ten. Ten frames are an excellent way to model the thinking process. For example, when we model 26+4 with a ten frame, it’s easy to see that we can shift the 4 dots over to completely fill three ten frames and make 30.
Find a unit for teaching the making multiples of ten strategy HERE.
Left to Right Addition
Left-to-right addition is a powerful mental math strategy for adding numbers with two or more digits. Place value understanding is key, as students will be grouping the tens and then the ones. For example, to solve 24+53, we will first add 20+50 to make 70, then 4+3 to make 7, and finally 70+7 to make 77. Left-to-right addition is important to teach BEFORE students learn the traditional algorithm. This is because left-to-right addition focuses on conceptual understanding rather than on the memorization of a series of steps.
Break Apart/Decomposing
Breaking apart an addend by place value is a powerful mental math strategy for adding numbers with two or more digits. Although this is similar to left-to-right addition, some students prefer it because only one addend is decomposed by place value, rather than both of them. For example, to solve 43+35, we could first decompose the 35 into 30 and 5. We start by adding 43+30 to make 73, then the remaining 5 to make 78.
Find a unit for teaching break apart HERE.
IN CLOSING
One of the greatest advantages of teaching your students mental math is that it teaches them to be flexible thinkers. When we only focus our math instruction on the traditional algorithms (carrying, borrowing, etc), we teach students to memorize a series of steps. If they forget those steps, they don’t know how to solve the problem. Mental math ensures that even if steps are forgotten, we possess the understanding that enables us to figure out the answer.
Math is not just a series of steps.
Mental Math is real understanding.

The Best Way to Teach Multiplication Facts: 12 Steps to True Understanding
Teaching multiplication is no easy task! Encouraging students to memorize the facts only allows a small percentage of them to be successful. Even then, those

Do You Need Help With Number Talks? Here’s The Quick Start Guide.
Number Talks have gained in popularity over the last several years – and for good reason! They are a powerful and collaborative way for students

Race to 100: A Hands-On Game for Addition to 100
Race to 100 (also known as The Trading Game) is a fun, two-player game for reinforcing addition and subtraction within 100. Even upper-grade students











8 Comments
This is exactly what I was looking for to guide my daughter…thanks for sharing such wonderful advice:) I like the way you build up the concepts…
These are terrific! I can’t wait to make them for my students!
Perfect timing!! My daughter is struggling with Mental Math. I know several of these tricks from my years of teaching, and of course my daughter doesn’t think I know! LOL. Now I can have her read the tricks and tips!! Thanks for making the cards and giving them away free!!
Wow! I always struggled with understanding math concepts as a child. I hated math, to the point of being in tears. As an adult, I am able to easily comprehend the strategies you are teaching. It is very thorough, yet simple. I LOVE it! I just got the cards so my kids can learn them. Thank you!
I have used these strategies all year long with my students and they have not only helped my students think of numbers in new ways, but have also helped me in my teaching! I feel like a much better math teacher now!
Any chance you have the exact same type of reference cards for subtraction?? That would be sweet! I’m changing grades next year and I know how valuable it would be for my students ever-changing needs. Fingers crossed! And can I just say that I’m glad you are Canadian!! 🇨🇦
Thank you for these great cards! I teach (or review if they learned them in previous grades) all of these strategies explicitly to my grade 3/4 students (and will at home with my own kids, as this has not been a focus at their school). As others have mentioned, I would love it if you had a set of these for subtraction too. These are handy also to pass onto EAs that find it challenging to work with students on mental math b/c they didn’t learn math this way 🙂
Hi Shelley , I can’t thank you enough for having your blog still available for us to use. I found my way while searching for help on doubles facts. This post alone, gave me reassurance on how I’m going about teaching math. Thank you so much!!!