
Left-to-right addition (also known as front-end addition or the partial sums method) is one of the most powerful mental math strategies for teaching addition of 2 or 3-digit numbers. However, many people are confused by why it is important and why it can be more effective than traditional vertical addition.
WHY IS LEFT TO RIGHT ADDITION SO EFFECTIVE?
The best part about left to right addition is that this strategy promotes real understanding.
When you solve an equation using the standard algorithm (probably the way that you learned to add multi-digit numbers), you use a series of steps. This includes adding the ones first, carrying if needed, then adding the tens, carrying if needed, etc. These steps are committed to your memory, and for those who have excellent memorization skills, this can be effective.
HOWEVER, the standard algorithm does not encourage understanding of place value and number sense. This is the main reason that today’s math instruction tends to shy away from the traditional algorithm in early grades. We want our students to possess REAL understanding of what they are doing. When students are taught methods that encourage mental math, they are able to think more flexibly not only about this isolated concept, but about other math concepts as well.
EXAMPLES
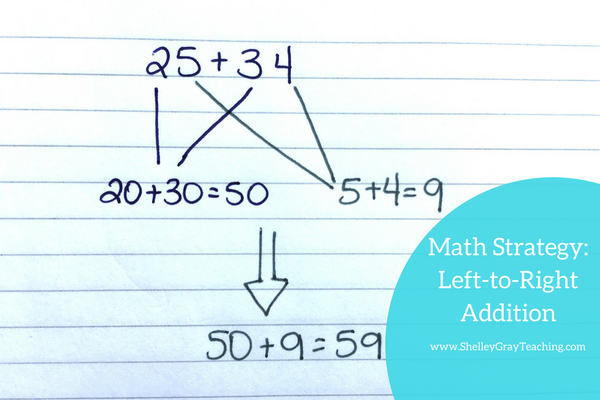
Left to right addition is also effective for adding 3-digit plus 3-digit numbers. In this example, we can see that we add the hundreds first, then the tens, and then the ones. Lastly, we add all of those sums together.

The CRA Model for Mental Math Strategies
NEXT STEPS:
- If you would like full support for teaching addition strategies in your classroom, check out The Addition Station HERE. You’ll find the left to right addition strategy in the Addition Stations for the upper grades. These Math Stations are self-paced, student-centered stations for the basic math strategies. Students move through the levels at their own pace, ensuring that they are always challenged, and working to their full potential.
- Read other posts on this website about addition strategies HERE.
- Download a FREE activity for practicing the left to right addition strategy HERE.
- Check out a Left to Right Addition Strategy Unit” HERE.
- Find task cards to reinforce the left-to-right addition strategy in isolation here:












6 Comments
Do you have similar posts for subtraction strategies?
Hi Cindy! I don’t have Subtraction Strategy posts at this time, but they are on my to-do list for the next couple of months! 🙂
Have a great day,
Shelley
I would also LOVE a subtraction strategy post 🙂
Thanks for this post!