
As a K-5 Math Consultant, I can’t tell you how many times I’ve heard a teacher say, “My students just don’t have number sense.” To be fair, I’ve said it during my teaching career as a special educator too. As teachers, we love to use this phrase when discussing math with our colleagues, our principal, and even with our students’ parents. We offer parents strategies to work with their child at home, and we provide Tier 1 interventions within the classroom to support this “missing” piece. But, as we discuss number sense in our math classrooms, there’s this ominous cloud that hangs over us:
What does it really mean, to have number sense?
Take a moment and reflect on this – the meaning of number sense.
What does it look like in your classroom?
What do you imagine when you are asked to describe a student who has number sense?
It’s difficult to put into words. I have these discussions every day with educators and I still struggle with this. I like to refer to the research from The National Council of Teachers of Mathematics to help guide number sense conversations. Here is what the NCTM has to say about number sense.
“As students work with numbers, they gradually develop flexibility in thinking about numbers, which is a hallmark of number sense… Number sense develops as students understand the size of numbers, develop multiple ways of thinking about and representing numbers, use numbers as referents, and develop accurate perceptions about the effects of operations on numbers.” NCTM Principles and Standards for School Mathematics, 2000
Notice some of the key takeaways:
- flexible thinking
- multiple ways of thinking about and representing numbers
- accurate perceptions about the effects of operations on numbers.
Number sense encompasses a multitude of mathematical ideas.

So, how can you support your students with numbers sense in a K-2 math classroom? Check out the Number Sense Trajectory below!
This progression was created from the work of John Van de Walle, Doug Clements, and Julie Sarama. Graham Fletcher also did a great video on the early number sense learning progression based on John Van de Walle, Doug Clements, and Julie Sarama’s work. It’s similar to other natural developmental progressions, such as a child first learning to crawl, then walk, run, skip, etc. Remember, in real life, some students may learn to walk before they crawl, so some of these concepts may come in a different progression. It all depends on the learner.
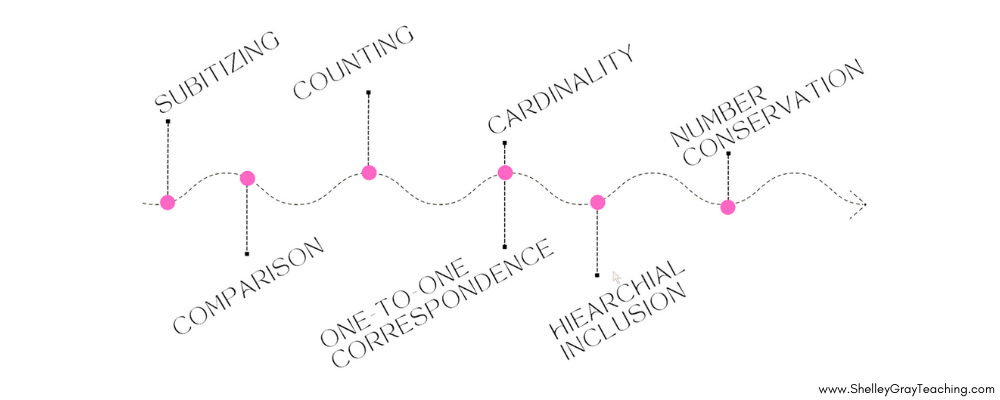
Before we dive into what each stage is, we must remember that number sense is not something that can be taught directly. As the NCTM definition states, students develop number sense as they begin to discover and understand the flexibility of numbers. Therefore this learning progression will help you understand what to look for when students first enter your classroom and how you can support students seeing numbers naturally.
It’s our job as teachers to provide students with opportunities to explore, visualize, and play with numbers.
Let’s dive in!
Subitizing
Flash this dot image to your students for 2-3 seconds and pose the question: “How many dots? “

Some students might count all to tell you how many, but some students may know instantly that it’s five dots. How do they know that? To be able to visually recognize a quantity of 5 or less is the power of subitizing. Kids start seeing objects as sets, or groups, and this helps students move past the 1:1 counting phase. The image above refers to our young learners, but as a teacher, I’m always wondering: How does this support number sense in the intermediate grades? Check out this dot image below:
Subitizing in the upper elementary grades can help elicit multiplicative thinking.

Related: Subitizing for Multiplication: Building Number Sense and Multiplicative Reasoning
Comparison
Children learn the concept of “more” at an early age: more food, more toys, more hugs, etc. This concept becomes generalized within their everyday life, and children are soon able to compare quantities by identifying which has more and which has less. This idea of comparison relates to concrete representations, like the one below.

Students can VISUALLY see the difference. It’s okay if they cannot tell you exactly how many! Students don’t need to count the objects at this stage. The focus at this stage is visual recognition, which ties in with subitizing.
Counting
Think of the alphabet song – our young learners can sing along, but do they really know that there are letters embedded in that song? The same goes for rote counting, which is the procedure of counting without meaning and understanding. In kindergarten, students learn the counting sequence from 0 to 100. Teachers introduce counting tools like a number path and a hundred chart to support the counting sequence.
One-to-One Correspondence & Cardinality
After children learn the rote counting sequence, we begin to introduce the idea of 1:1 correspondence. This means students can connect one number with one object and then count them with understanding. We can build this idea not only with number matching, but also with object matching, like the image below. We want to elicit the idea that we can match 1 star to 1 cube.

1:1 correspondence may take time and we need to make sure we are giving students the opportunities to explore and practice. While children are learning about 1:1 correspondence, they are simultaneously exposed to the idea of cardinality: to tell how many things are in a set. When counting a set of objects, the last word in the counting sequence names the quantity for that set.
Hierarchical Inclusion
Hierarchical Inclusion sounds like a complicated concept, but it’s something that children will discover when practicing counting and 1:1 correspondence. It means that numbers are nested inside of each other and that the number grows by one each count. For instance, 4 is inside 5 or 5 is the same as 4 + 1.

You can practice this concept by asking students to count out a set of 7 objects. Then, ask the students to use that set to show a smaller set of 5 objects. Instead of counting out a whole new set, students with hierarchical inclusion will know that they can take 5 counters from the 7 to make the new set. Concrete representations are extremely important at this level of learning.
Number Conservation
The big idea of number conservation is derived from hierarchical inclusion. Students at this level of learning begin to understand that there is a decomposition of numbers. Number conservation means that the number of objects remains the same when they are rearranged spatially. Let’s look at the example below. You may ask your students: Are these the same?

Yes! These are the same. Students relate this arrangement to 1:1 correspondence. Now, show students the image below and ask: “Are these the same?”

Some students may say no, there are more lightning bolts. These students do not understand the concept of number conservation yet. Continue to expose students to objects in a variety of arrangements and continue to connect this idea to 1:1 correspondence.
Now What?
You may be thinking, “This is great information, Allison, but what does that look like as instruction in my classroom?” There are so many activities you can do to help support your students’ number sense in the math classroom! I’ll be sharing some activities you can do with just double ten frame cards for each phase of this learning progression soon. If you already have some activities/lessons, feel free to share in the comments below. We are better teachers together!
Grab and Go
K-2 Learning Trajectory Document
Graham Fletcher- The Progression of Early Number Sense and Counting (video)
Deep Dive
Learning and Teaching Early Math: The Learning Trajectories Approach by Clements & Sarama
Teaching Student Centered Mathematics PreK-2 by Van de Walle & Friends







