How to Teach the 9 Times Table So It Really Makes Sense

There are many tricks out there for the 9 times table. But be careful before you teach these in your classroom. Remember – there are strategies, and then there are tricks. A strategy will enable you to solve ANY problem. A trick is typically limited to only certain problems. Do you want to limit your students? Or do you want to enable them to solve any problem?

Ok, let’s take a look at some of the popular ways to teach the 9’s facts. I do not endorse all of these – but I do want you to be aware of them if you are not already.

 

TRICK #1 (NOT A FAN OF THIS ONE)

If you want to multiply 9×4, you put down your fourth finger.

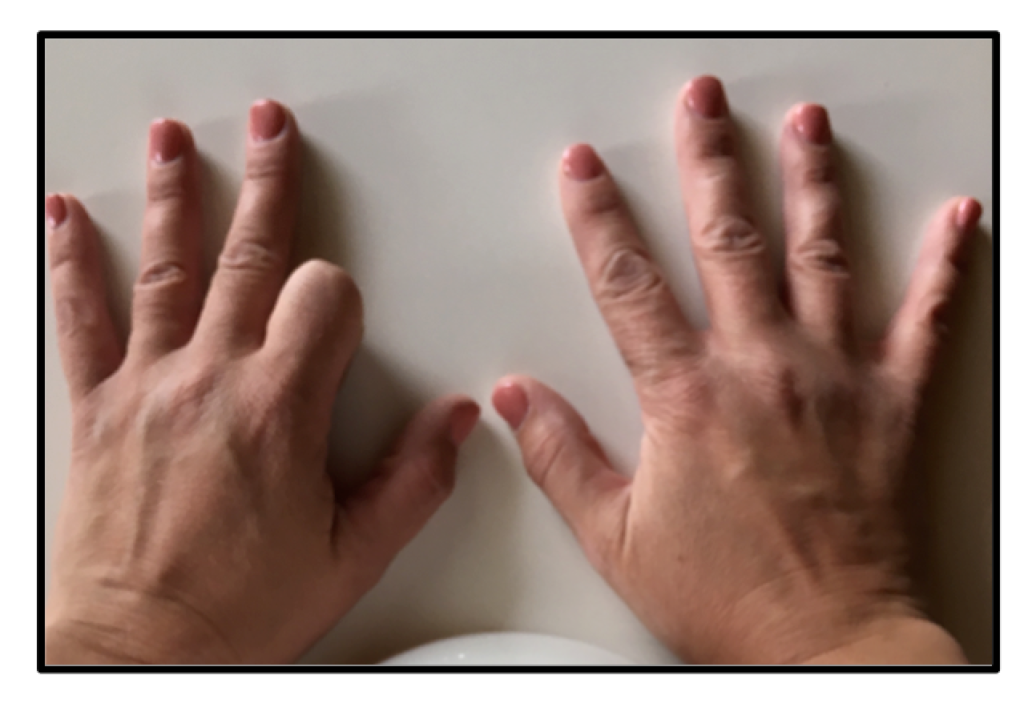
Then you are left with 3 fingers on one side, and 6 fingers on the other. So the product is 36.

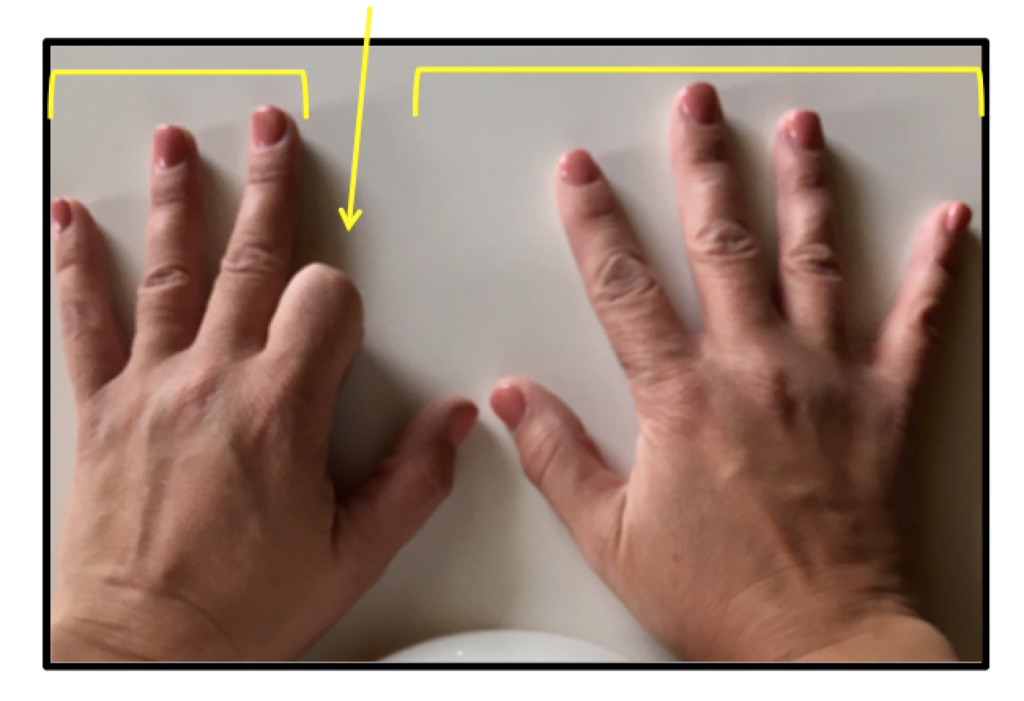
If you want to multiply 9×8, you put down your eighth finger.

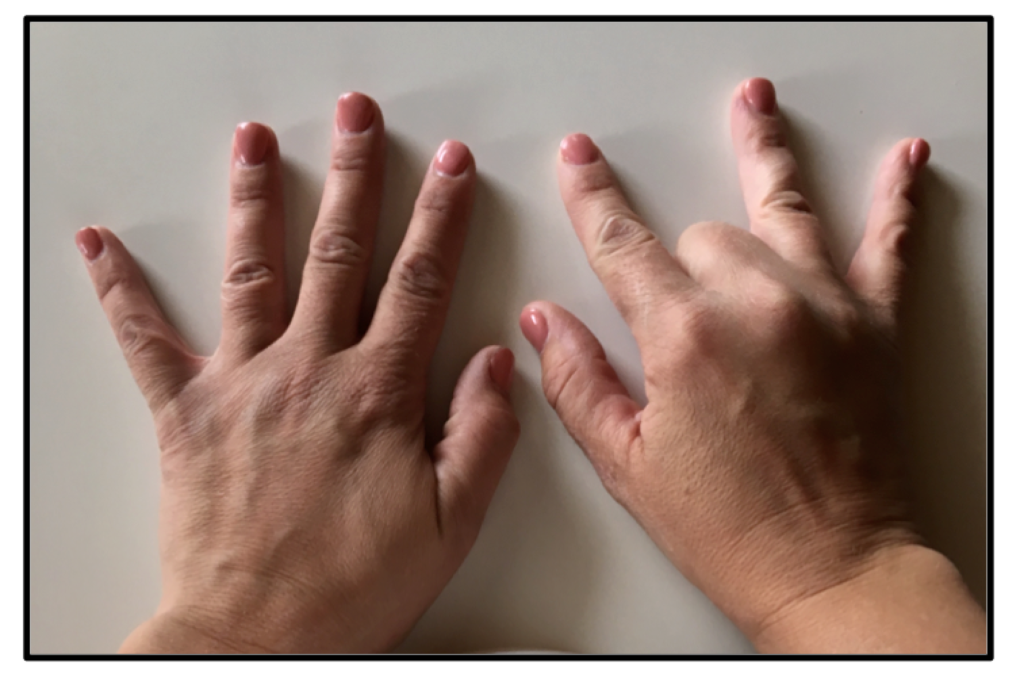
Then you are left with 7 fingers on one side, and 2 fingers on the other. So the product is 72.

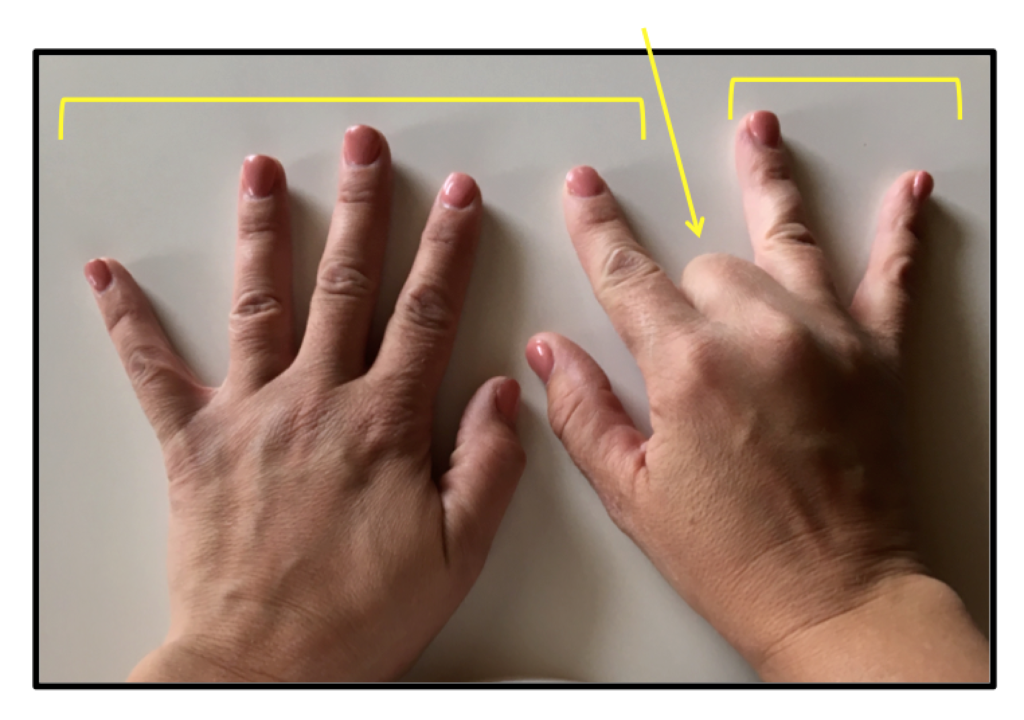
So I’ll admit that this is kind of a neat trick. However, I just don’t like my students to rely on their fingers. I feel like we are always trying to get our students AWAY from finger counting as a strategy, so I’d rather not have them rely on this one.

 

TRICK #2

Here’s another trick that I don’t like:

For this one, we list the numbers from 0-9, and then list the numbers from 9-0 beside that.

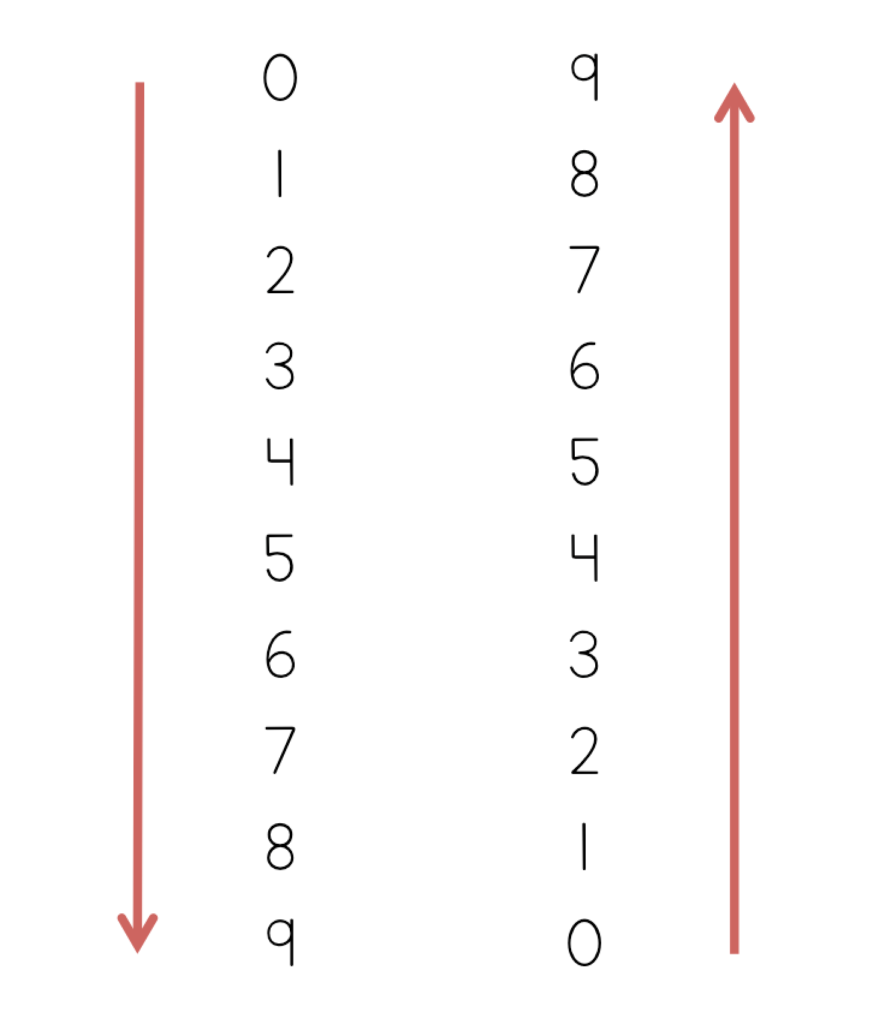
Now you’ll see that this shows all of the products of the 9’s facts from 0-10. For example, the second row down shows the product of 9 and 2:

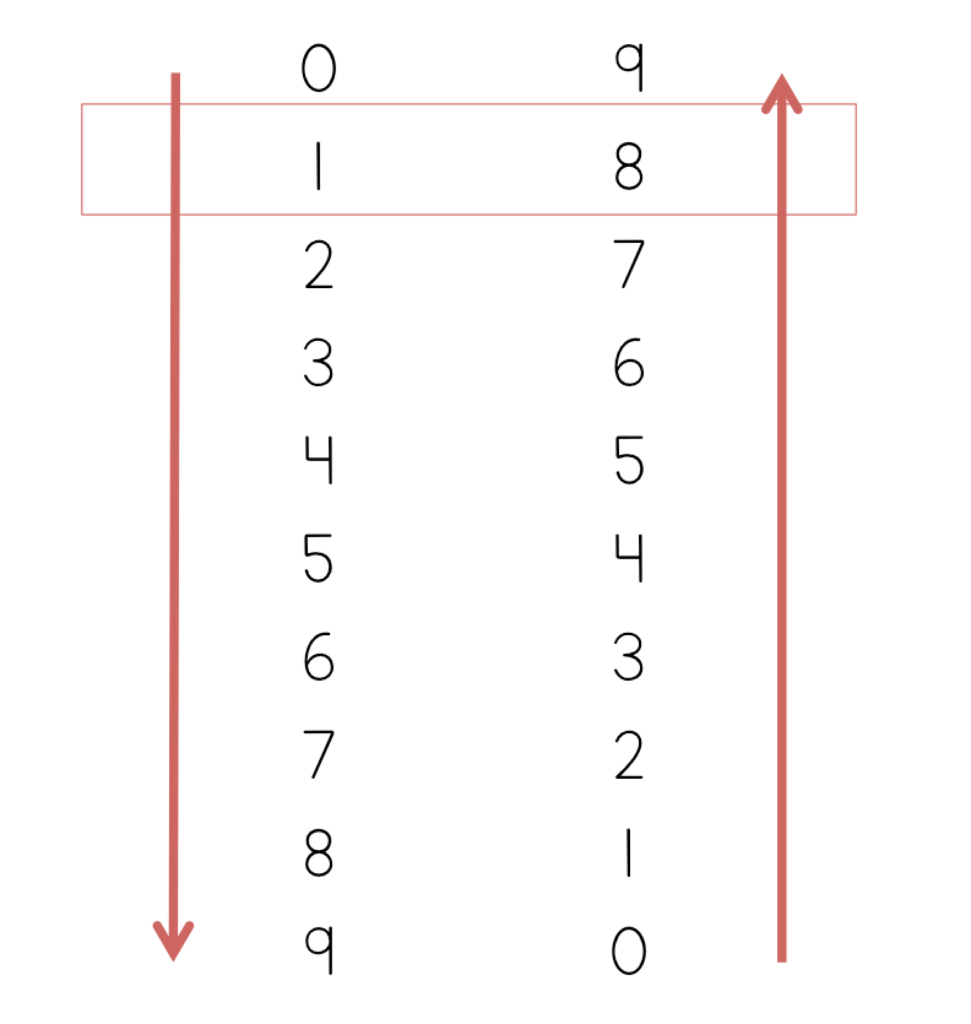
The sixth row down shows the product of 9 and 6:

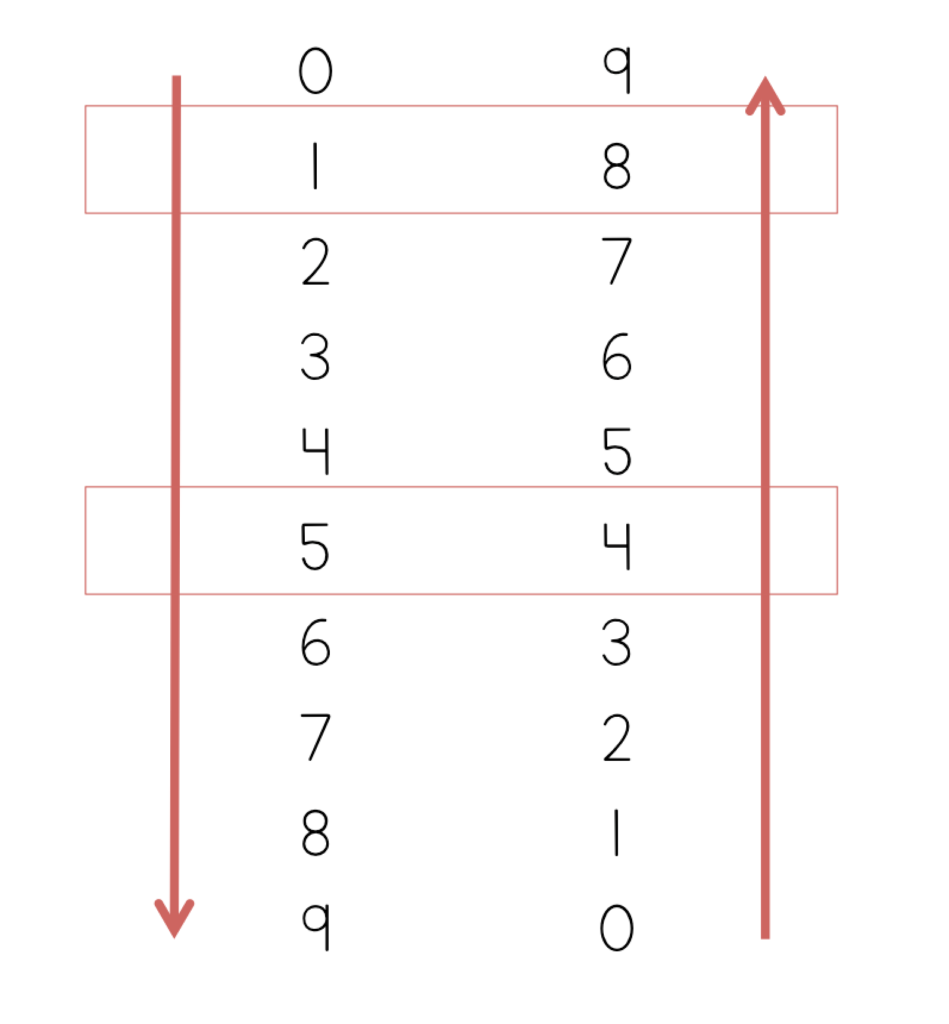
So again, this is a neat trick, but in my mind it’s not practical. When my students are faced with a 9’s equation, the last thing that I want them to do is take 3 minutes to list out all of the numbers, and then count the rows down to figure out the product. Also, does this enable them to solve a problem like 9×25? No. This is a limiting trick.

 

TRICK #3

This is a trick that I actually like because it is FUN, motivating, and SO fast once you get the hang of it….but read to the end for the down side to this one.

What do you notice about the products below?

9×1=9

9×2=18

9×3=27

9×4=36

9×5=45

9×6=54

9×7=63

9×8=72

9×9=81

9×10=90

So what do you notice? In every product, the digits can be added together to make 9. Students have to remember this.

Here’s how to perform the strategy:

Step One: Look at the equation. Point to the number that is NOT the 9. For example, in the equation 9×4=___, point to the 4.

Step Two: Subtract 1 from the number that you are pointing to. In this example, you would think “4-1=3.” The difference (in this case, 3) will be the first number of your product. So now our equation looks like this: 9×4=3__.

Step 3: When you add the numbers in the product together, they will make 9. So now we need to think, “What can I add to 3 to make 9?” In this case the answer is 6. Add this 6 as the second digit in your product: 9×4=36.

Let’s try another one: 9×8.

Step One: Look at the equation. Point to the number that is NOT the 9. For example, in the equation 9×8=___, point to the 8.

Step Two: Subtract 1 from the number that you are pointing to. In this example, you would think “8-1=7.” The difference (in this case, 7) will be the first number of your product. So now our equation looks like this: 9×8=7__.

Step 3: When you add the numbers in the product together, they will make 9. So now we need to think, “What can I add to 7 to make 9?” In this case the answer is 2. Add this 2 as the second digit in your product: 9×8=72.

As you can see, this works with any basic multiplication fact involving a 9. Notice that in every case, the sum of the numbers in the product add up to 9!

 

But let’s talk about the downside to this trick.

Does it enable them to solve a big equation like 9×25? No. So even though this trick is fun (and I still use it!), it limits our students in terms of the problems that they can solve.

 

Now, let’s talk about a STRATEGY.

 

EFFECTIVE STRATEGY

This next strategy is a true mental math strategy. This is one that you’ll want to introduce your students.

We know that the 10’s multiplication facts are an easy set to learn. So for the 9’s facts, we can use a 10’s fact, and then just subtract one group.

For example, for 9×3, first do 10×3 to make 30, and then subtract one group of 3 to make 27.

For 9×7, first do 10×7 to make 70, and then subtract one group of 7 to make 63.

This is a strategy that enhances conceptual understanding. Students should be able to visualize in their heads the idea of having 10 groups and then simply taking away one group.

We know that tricks are limiting. How about this strategy? Can it be used with a problem like 9×25? Absolutely! Let’s start with 10 groups of 25 to make 250 and then simply take away one group of 25 to make 225.

 

 

CONCLUSION

When you teach multiplication in your classroom, always focus on conceptual understanding FIRST. Before any tricks, ensure that your students really grasp what multiplication means. If you want to teach them neat tricks later on, use your professional discretion, but always begin with strategies that promote real understanding and that do not limit students in terms of what they can solve.

 

 

 

NEXT STEPS

 

• Reinforce the 9’s multiplication facts with this set of task cards. Students will learn conceptually through problem-solving, using arrays, strategic thinking, finding missing numbers, skip-counting, picture representations, and more:

 

 

OR FIND THE FULL BUNDLE OF MULTIPLICATION TASK CARDS HERE.

 

Or choose from the following recommended resources for teaching multiplication fact mastery:

The Multiplication Station: A Self-Paced, Student Centered Program for Basic Multiplication Facts

Multiplication Strategy Posters

Multiplication Equation of the Day Booklet