
Long division is often considered one of the most challenging topics to teach. Luckily, there are strategies that we can teach to make multi-digit division easier to understand and perform.
The Grid method is one of these strategies.
The Grid Method is intended for those who plan to teach traditional long division. It follows the same steps as traditional long division, but uses a different method of organization. This makes traditional long division easier for some students.
The Grid Method is not a mental math based approach. If you are looking for a mental math approach to long division, be sure to check out my posts for the Box/Area Method and Partial Quotients.
Let’s learn how to perform the Grid Method for long division!
Below, I have included both a video tutorial and step-by-step instructions.
VIDEO TUTORIAL:
STEP-BY-STEP INSTRUCTIONS
Suppose that we want to solve the equation 324÷2.
STEP 1:
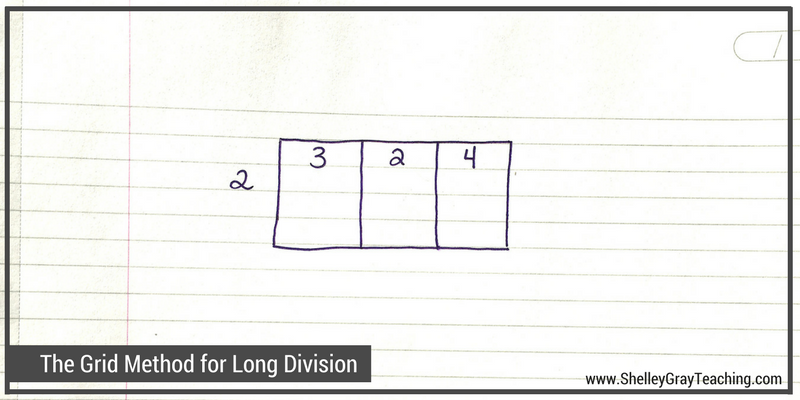
First we draw a grid. The number of sections in the grid depends on the number of digits in our dividend. For this equation, our grid will have 3 sections. We write the digits from 324 inside the grid, and we write our divisor (2) on the left side.
STEP 2:
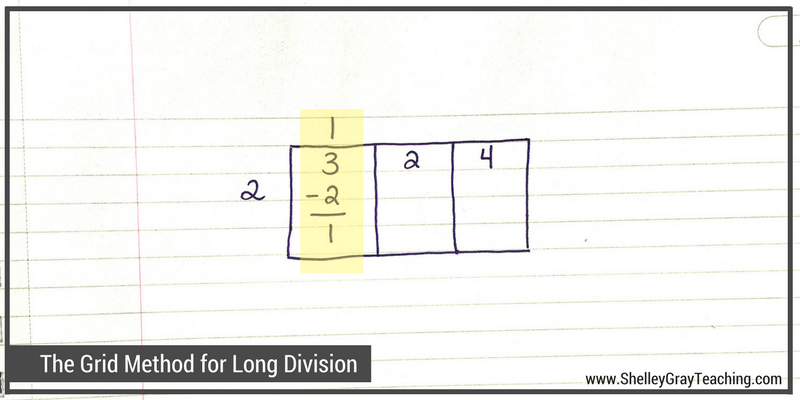
Now we ask ourselves, “How many times can 2 go into 3?” The answer is 1, so we write a 1 on top of the grid. We now multiply 1×2 to make 2, and take that 2 away from the 3. This leaves us with 1.
STEP 3:
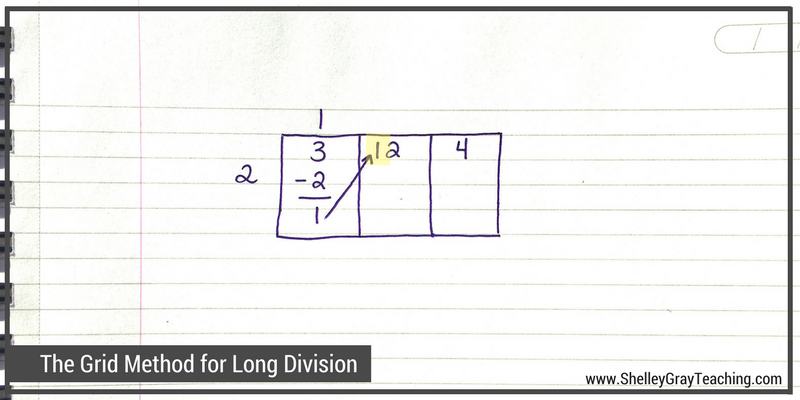
Now we bring that 1 over to the tens place of the next section on the grid. This gives us a 12 in the next section.
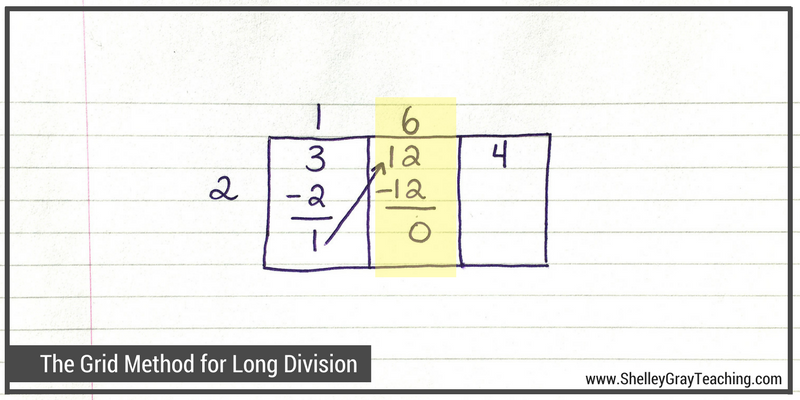
Now we ask ourselves, “How many times does 2 go into 12?” The answer is 6, so we write a 6 on top of the grid. Now we multiply 6×2 to make 12, and take that 12 away from 12. This leaves us with 0.
STEP 4:
We carry that 0 over to the tens place of the next section on the grid. This doesn’t affect that number, so we still have 4 in the next section.
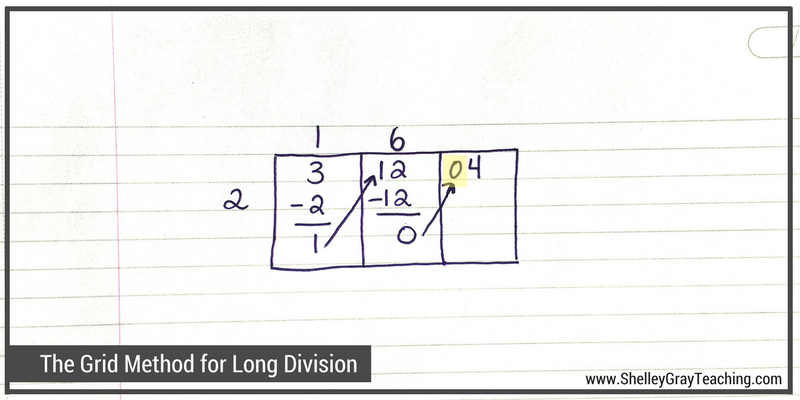
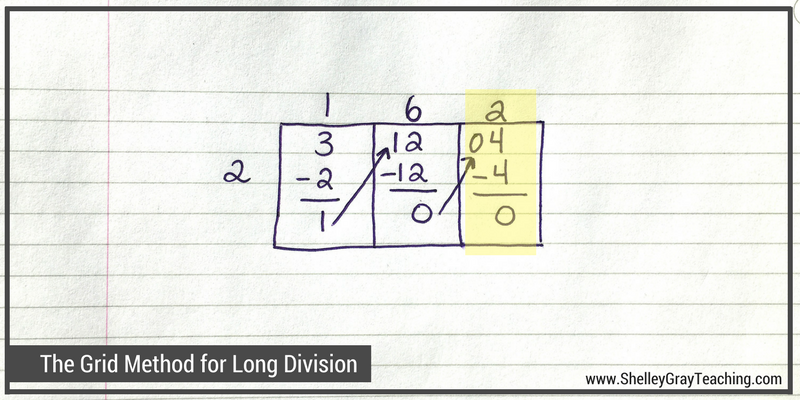
Now we ask ourselves, “How many times does 2 go into 4?” It goes 2 times, so we write a 2 on top of our grid. Now we multiply 2×2 to make 4, and take that 4 away from the 4. We are left with 0, which means that we have no remainder.
To find the final quotient, we simply list the digits from the top of the grid: 1, 6, 2. So 324÷2=162.
LET’S TRY ANOTHER EXAMPLE
This time we will try an example that has a remainder. It also has more digits that our last example. Notice that when we have more digits in our dividend, we simply extend our grid. Let’s solve 6542÷5.
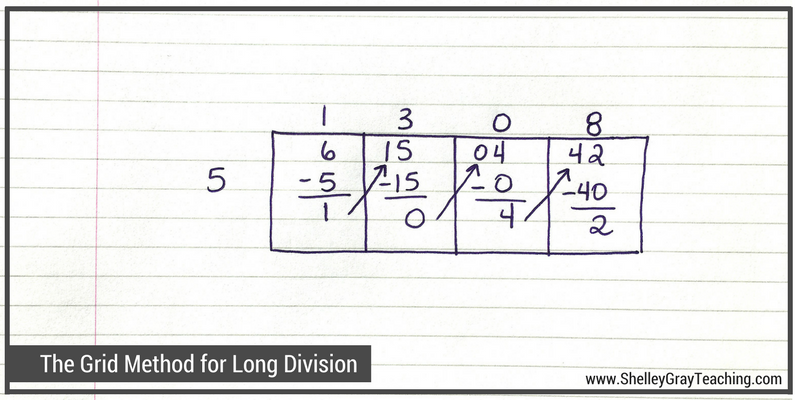
Here are the steps that we followed to solve this equation:
- Section 1: First we knew that 5 goes into 6 one time, so we wrote a 1 on top. We multiplied 1×5 to make 5, and took that 5 away from the 6, leaving us with a 1. We carried that 1 over to the tens place of the next section. Now we have 15 in that section.
- Section 2: We know that 5 goes into 15 three times, so we wrote a 3 on top. We multiplied 3×5 to make 15 and took that 15 away from the 15, leaving us with 0. We carried that 0 over to the tens place of the next section.
- Section 3: 5 does not go into 4, so we write a 0 on top, multiply 0x5 to make 0, and take that 0 away from the 4. This leaves us with 4. We carry that 4 over to the tens place of the next section, giving us 42 in the final section.
- Section 4: 5 goes into 42 eight times, so we write an 8 on top of the grid. We multiply 8×5 to give us 40, and take that 40 away from the 42, leaving us with 2. This means that our remainder is 2.
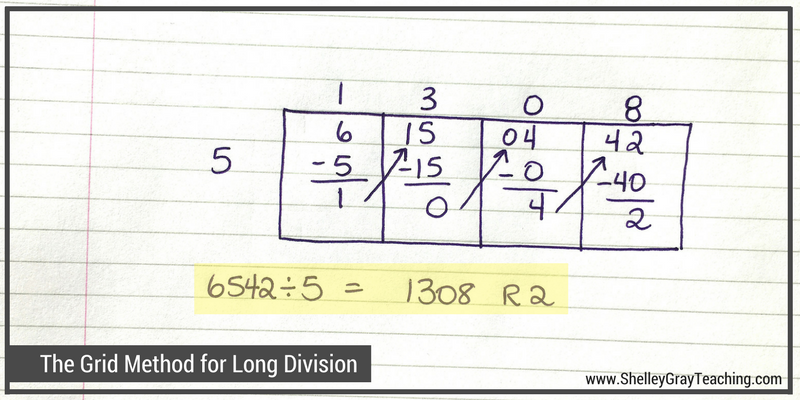
- To find our final quotient, we list the numbers from the top of the grid: 1, 3, 0, 8, and then add our remainder of 2. So 6542÷5=1308 R2.
NEXT STEPS:
I would love to help you teach the grid method and other division concepts in your classroom. You may find the following resources helpful:
GRID METHOD TASK CARDS
These task cards give students the opportunity to practice the grid method for long division in a variety of different ways. Students will calculate quotients, solve division problems, figure out missing dividends and divisors, think about how to efficiently solve an equation using the grid method, and more. See the Grid Method Task Cards HERE or the Big Bundle of Long Division Task Cards HERE.
THE LONG DIVISION STATION
The Long Division Station is a self-paced, student-centered math station for long division. Students gradually learn a variety of strategies for long division, the grid method being one of them. One of the greatest advantages to this Math Station is that is allows you to target every student and their unique abilities so that everyone is appropriately challenged. See The Long Division Station HERE.









12 Comments
I was wondering if there is a way to do problems such as 409 divided by 12? I’m looking for an easier method to do harder problems. Thank you!
I am concerned with teaching the grid method as a strategy for the division. Base ten place value and the ten to one relationship is an integral concept for whole number and decimal number computation. The grid method seems to be a trick or graphic organizer and does not bring out the place value or the relationship among the places, certainly, it does not conform with the “teaching for understanding” goal. Sadly, even though we encouraged preservice and in-service to carefully take advice or activities from the internet without investigating the research base they are busy and assume if it is on the web it must be OK. As a long time mathematics educator, I am concerned that the grid method is included in this posting.
Hi Vickie! Yes, you are correct in saying that this method does not use place value understanding. In the beginning of the blog post, that’s why I mentioned that this is NOT a mental math based approach, but can be used for those who are planning on teaching traditional long division (which also does not rely on place value understanding). I also address this in the video, but I’ll try to edit this post to make it more clear. I absolutely agree with you that teaching for understanding is vitally important. In this blog post I also link to posts on the partial quotients and box methods, which are much more mental math focused.
I like to show my students a variety of methods for dividing. Sometimes, you can teach them with conceptual understanding of place value time and time again, and they still don’t get it. I NEVER think teaching a different method, after you introduce using conceptual understanding, is a bad thing. You might actually have students who finally get it, and that is always a good thing.
I couldn’t disagree more. This method is 💯 rooted in place value. Each digit is in its own place value box. You could put all the zeroes in there (expanded form) for explaining purposes but then get them out to simplify the process. I substitute the numbers in the boxes with place value blocks on day 2 or 3 so they can see how this method is based on place value. It works well for showing why you regroup the leftover value as you move to the right. Don’t knock something until you try it and evaluate it thoroughly. This method is wonderful and there’s no reason to learn the standard way. This IS the standard way with a little extra organization.
You are correct in saying that this method doesn’t emphasize thinking about place value. However, does the standard algorithm really require thinking about place value? Most kids don’t even realize that they are working with place value. Asking “How many times does 12 go into 48?” pays no attention to whether that is 4800 or .048. It is only when students are asked to understand more deeply why the algorithm works that they focus on place value.
This method does not simplify using the long division algorithm and is less for working with multi-digit problems, so as Shelley says, it is a great intro to help kids break down the long division algorithm before learning it. I would add that this structure could also be used to teach polynomial division, as each term could go in its own distinct box.
I love this method. I think it will really help my scholars who are having trouble with long division. I have tried many methods and I am excited about trying this one! I also purchased your resource on TpT. Thanks again!
LOVE THIS!!! One of my students who struggles terribly with math was so excited to succeed with this today 🙂
One question: Does this method work with a divisor larger than one digit? The video only demo’d one-digit divisors.
I am trying to learn this method to better learn how to help my daughter who is learning this method in school.
@J Riley i figured out a way to do this method with multi-digit divisors i will try to explain without the use of actual boxes. (lets assume each line is a new box each R will move into next box as normal)
12/6725=?
12 / 67 = 5 R7
12 / 72 = 6 R0
12 / 05 = 0 R5 (at this point we have a remainder of 5)
so our answer is 560 R5
lets try a 3 digit divisor
120 / 64925 = ?
120 /649 = 5 R49
120 / 492 = 4 R12
120 / 125 = 1 R5
so our answer is 541 R5
as you can see from the examples for 2 digit divisors, divide first into the first 2 digits (if it will go , if not read further).
For 3 digit divisors divide first into the first 3 digits ( if it will go , if not read further)
now lets try an example where you can’t follow these steps
34 /12465 = ?
34 / 124 = 3 R22
34 / 226 = 6 R22
34 / 225 = 6 R21
so our answer is 366 R21
all you do is divide first into the first 3 digits
remember each line is a different box in the box method so how i recommend teaching this with multi-digit divisors is instead of creating multiple boxes at the start create a new box each time you need one.
Maybe Shelley Gray could create an example on the website that reflects this? but in the meantime just use the above examples try on a piece of paper recreating my examples in boxes ( remember each line is a new box).
I know without a graphic “box” it maybe hard to visualize but try it out its the same principle just where you start whether you divide into the first digit or the first 2 digits etc.
I hope this helps 🙂
I DO see place value in this method, as long as it is explained to the students. In the example above, the left-most box is the thousands place. After dividing the 6 thousands by 5, there is 1 thousand remaining. Regroup that thousand into hundreds. (There are 10 hundreds in 1 thousand. Add the 10 hundreds to the 5 hundreds already in the hundreds box.) And so forth.
It was very easy for me to explain this method to my son using place value, so that he understands why the process is working. Taking the first example 324 ÷ 2.
How many hundred times will 2 go into 300? We say how many hundred because this is the number we are going to write in the hundreds place. We can say how many times does 2 go into 3, and then multiply that by 100. It will go in 1 hundred times. We’ll write a 1 in the hundreds place.
100×2 is 200, so we’re going to subtract a 2 in the hundreds place. That’s the part we’ve already used. So now we have 1 hundred left. We’ll bring that 100 into the tens place. So now in the tens, we have 120 which we’re calling 12 tens. In the tens place, how many times can 2 go into 12 tens? 6 times. Since that’s in the tens place, it means 60, and 2 x 60 is 120.
And so on. My son’s really solid on place value and the meaning of each digit, so this explanation worked beautifully for him, and was much easier to visualize than if I’d used the same teaching style with the traditional method. It’s also more efficient to write, and leaves less room for copying or place value errors than partial quotient. It also lends itself much more easily to decimals than does partial quotient. All this is important because he is dysgraphic. The less he needs to write and line up, the better.
Very helpful! Thank you so much! My students will do really well with this. 🙂